Dyskretny problem plecakowy to kolejne zagadnienie algorytmiczne, które zaraz wyłożymy profesjonalnie, jak na właściciela strony przystało 😁! Serdecznie zapraszam po "odbiór" wyjaśnień, jak i samego kodu źródłowego ❤️! Wchodzisz 🙂?
DYSKRETNY PROBLEM PLECAKOWY. W ROLACH GŁÓWNYCH: PLECAK I PRZEDMIOTY!
Problem o podanym tytule jest zagadnieniem optymalizacyjnym polegającym na wyborze takiego zbioru przedmiotów, aby suma ich wartości przyniosła największe zyski 💵. Całą sprawę komplikuje fakt, iż suma ich wag nie może przekraczać pewnego progu 🔒. Czyli mamy funkcję celu (jak to ładnie określają matematycy 😊) i ograniczenie 🚧.
Dyskretny problem plecakowy charakteryzuje się postawieniem 2 ważnych pytań 👇:
- które przedmioty zabrać, aby zmaksymalizować zyski (w dowolnej formie)?
- które przedmioty zabrać, aby wszystkie "zmieściły się" w plecaku?
Wyobraź sobie złodzieja, który czai się na czyjąś posesję, aby ukraść "legalnie" czyjeś własności 🥷🏾. Włamuje się do domu i zastanawia się które przedmioty schować do plecaka, aby przyniosły największy zysk w złotówkach, gdyby znalazł się na nie jakiś kupiec 🤑. Nie może wziąć wszystkiego jak leci, bo plecak ma ograniczoną pojemność 👜. Zatem, bierze tylko te przedmioty, które wszystkie razem wzięte się zmieszczą w plecaku, a potencjalny z nich zarobek będzie jak największy 💵. Tak można by "ubrać" dyskretny problem plecakowy (ang. discrete knapsack problem) w historyjkę (ale nie dla dzieci 😝) 😁.
Niestety ten problem nie jest taki łatwy do rozwiązania, jak może Ci się wydawać 😳...
ANALIZA DYSKRETNEGO PROBLEMU PLECAKOWEGO
Załóżmy, że wokół siebie mamy pewne przedmioty do wyboru. Każdy z przedmiotów jaki ma grać istotną rolę w rozstrzygnięciu jego wzięcia czy pozostawienia, musi posiadać 2 zdefiniowane cechy 👇:
- wartość,
- waga.
Kontekst wartości zazwyczaj nadajemy w ujęciu finansowym (aczkolwiek wcale nie musi takie być!) 💰. Dla prostego przykładu, trzymajmy się waluty PLN 🙂. Waga intuicyjnie jest odbierana jako ciężar (choć nie musi tak być 😉), dajmy sobie kilogramy 💪.
Gdybyśmy chcieli zrobić sobie proste zestawienie naszych obserwacji, to możemy ująć to następująco:
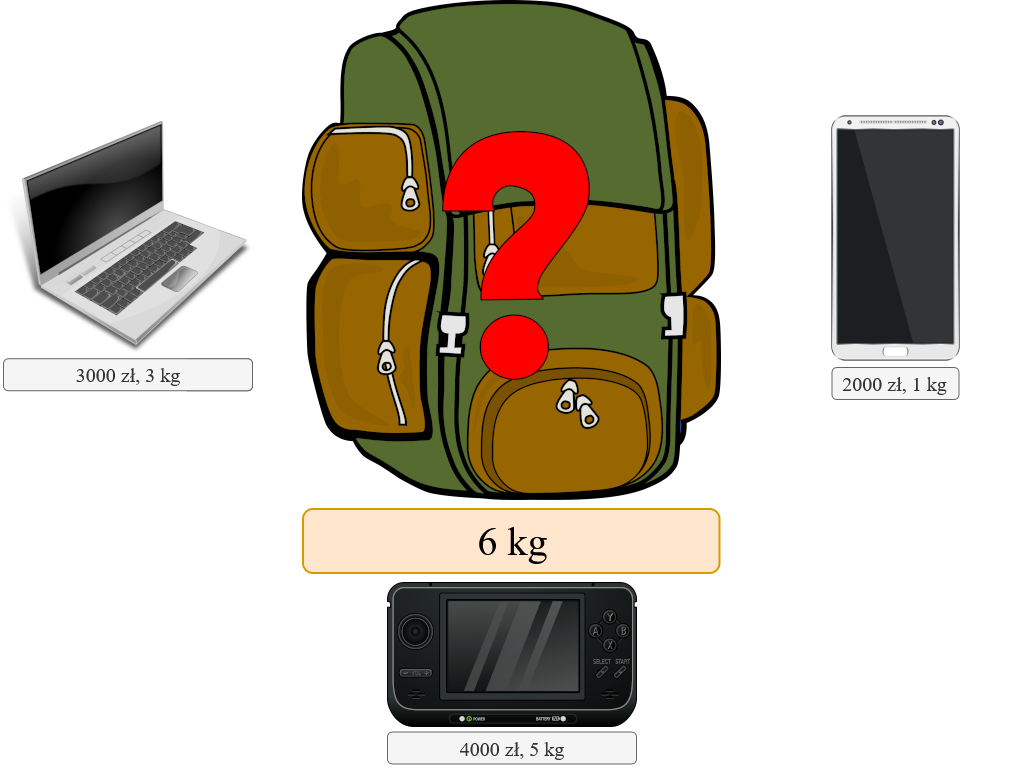
| Przedmiot | Wartość [zł] | Waga [kg] |
| Laptop | 3000 | 3 |
| Smartfon | 2000 | 1 |
| Konsola do gier | 4000 | 5 |
A teraz drugi "bohater", plecak 👜! Plecak ma tylko jedną cechę, która realnie wpływa na rezultat: pojemność 💥! Dajmy na to, że nasz plecaczek dysponuje pojemnością równą 6 kilo 6️⃣.
Teraz stawiamy kluczowe pytanie: jak ocenić jaki podzbiór przedmiotów zmaksymalizuje zyski, aby suma ich wag była nie większa niż 6 kilogramów?
Na pewno da się to jakoś ustalić. Tylko jak 🤔?
Problem: wyznaczenie podzbioru przedmiotów o największej wartości sumarycznej nieprzekraczającej pojemności plecaka
Muszę sprawić przykrość 😐. Wyznaczenie konkretnego podzbioru jako optymalne dobranie odpowiednich przedmiotów, jest możliwe wyłącznie po sprawdzeniu wszystkich kombinacji 😓. Zatem, dostępna jest tylko metoda "brute-force", tak jak przy problemie komiwojażera 😱!
Złożoność czasowa będzie nie do zaakceptowania (według notacji dużego O jest ona wykładnicza i zaraz się dowiesz dlaczego ⚠️!), problem jest NP-zupełny, a metoda jest nieefektywna dla dużych zbiorów danych 😨!
Ustalmy dlaczego tak się dzieje 🔥.
SKĄD BIERZE SIĘ ZŁOŻONOŚĆ WYKŁADNICZA?
Zacznę od stwierdzenia faktu - w notacji dużego O, złożoność czasowa wygląda następująco 👇:
O(2n)
N-ta potęga liczby 2, czyli inaczej, 2 podniesione do potęgi równej liczbie elementów 💥!
Aby pojąć dlaczego tak, a nie inaczej, musisz przypomnieć sobie z matematyki takie terminy, jak:
- permutacja bez powtórzeń,
- zbiór potęgowy.
Skorzystajmy z tabelki u góry 👆.
Dla 3 przedmiotów, konieczne jest przeanalizowanie 8 kombinacji, czyli 23 ℹ️. "Dwójka" jest dlatego, że dla każdego przedmiotu, musimy się opowiedzieć czy go bierzemy (1), czy nie (0). Powstaje "zerojedynkowa decyzja" i nie ma żadnych innych możliwości 💡.
W dyskretnym problemie plecakowym, rozpatrujemy każdy przedmiot jako całość ⚠️. Nie badamy możliwości wzięcia połowy czy jakiegoś ułamka - albo bierzemy cały przedmiot, albo nie bierzemy go wcale.
Jeżeli zatem, każdy przedmiot możemy wybrać albo nie i trzeba podjąć decyzję dla wszystkich elementów zbioru, to powstanie nam taki oto zbiór potęgowy, czyli zbiór wszystkich podzbiórów zbioru przedmiotów 😅:
P(I) = {{0,0,0}, {0,0,1}, {0,1,0}, {1,0,0}, {1,0,1}, {1,1,0}, {0,1,1}, {1,1,1}}
Przedstawię to samo na tabelce, powinno być lepiej widoczne do czego zmierzam 🙂:
| Lp | Laptop | Smartfon | Konsola do gier |
| 1 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 |
| 3 | 0 | 1 | 0 |
| 4 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 |
| 6 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 |
| 8 | 1 | 1 | 1 |
Teraz widzisz o co się rozchodzi 🎯! 8 kombinacji, jako zestawienie wszystkich dostępnych możliwości 🔀. "Binarna" decyzja (bierzemy przedmiot lub nie), N przedmiotów do analizy i wszystko się zgadza ✔️! Stąd złożoność czasowa jest równa N-tej potędze liczby 2 😞!
 |
Dyskretny problem plecakowy to problem NP-zupełny, w którym próbujemy rozstrzygnąć które przedmioty włożyć do plecaka, aby zmaksymalizować zyski i żeby suma ich wag nie przewyższyła maksymalnej pojemności plecaka.
MUSI CI WYSTARCZYĆ ROZWIĄZANIE PRZYBLIŻONE
Trzeba szukać szczęścia w aproksymacji 🤷♂️. Jak przy problemie komiwojażera, tutaj również jest wiele podejść do implementacji przynoszących rozwiązanie zbliżone do idealnego ✅. A ja poczęstuję Cię taką, która korzysta z programowania dynamicznego, o którym szepnąłem parę słów więcej w osobnym artykule 🤩! Wprowadzę Cię w metodykę działania 😎.
Programowanie dynamiczne charakteryzuje się dzieleniem zadanego problemu na mniejsze "podproblemy", natomiast to nie działa tak samo, jak "dziel i zwyciężaj" ⚠️. Cechą programowania dynamicznego jest przechowywanie rozwiązań "podproblemów" w tabelce albo siatce ("memoizacja"), a te "podproblemy" są rozwiązywane progresywnie, czyli rezultaty rozwiązań kolejnych "podproblemów" są zależne od wcześniej otrzymanych wyników 📝.
Dużym plusem programowania dynamicznego jest zmniejszenie złożoności czasowej 👍. Algorytm chcąc rozwiązać kolejny "podproblem" przy którym się znajduje, nie musi ponownie wyliczać wszystkiego od zera, tylko sobie "sięga" do tabelki i pobiera wynik, który zostaje później zastosowany do rozwiązania aktualnej części problemu 📈. Minus? Narażamy się na bardziej lub mniej znaczący margines błędu 😏. Gdyż to jest algorytm aproksymacyjny 😊!
Teraz wytłumaczę jak można rozwiązać dyskretny problem plecakowy z użyciem programowania dynamicznego 🚀!
SIATKA "PODPROBLEMÓW"
Nasza siatka będzie składać się z wymiarów o następujących znaczeniach 👇:
- wiersze = podzbiory przedmiotów,
- kolumny = pojemności "podplecaków".
Wiersze będą reprezentować podzbiory przedmiotów, w których znajdą się tylko te elementy, których indeks w kolejności nie przekracza numeru wiersza. Czyli dla pierwszego wiersza, będzie przypisany podzbiór jednoelementowy, w którym znajdzie się tylko laptop (nasz pierwszy przedmiot w kolejności) 💻. Kolumny określają pojemności "podplecaków" rosnące o jedną jednostkę do góry, aż do rozmiaru całego plecaka 💯. Wiem, że na pierwszy rzut oka to brzmi komicznie 🤭, natomiast jak zobaczysz na czym polega wpisywanie wartości do siatki, to dostrzeżesz w tym sens 💡.
Mamy 3 przedmioty, więc będą 3 wiersze 3️⃣. Mamy plecak o pojemności 6 kilogramów, zatem pojawi się 6 kolumn 6️⃣.
Trzeba jeszcze wspomnieć o samych komórkach, które będą oznaczały wartość sumaryczną przedmiotów dla danego podzbioru przy posiadaniu danego "podplecaka" 🔥. To będą rozwiązania częściowe (lokalnie optymalne rozwiązania), bo każda taka wartość, to będzie krok bliżej do otrzymania rozwiązania ostatecznego, którym będzie ostatni rząd i kolumna 🔔.
DZIAŁANIE PROGRAMOWANIA DYNAMICZNEGO DLA DYSKRETNEGO PROBLEMU PLECAKOWEGO
Zaczynam tłumaczyć działanie krok po kroku ❤️! Nasze wcześniejsze ustalenia, wpisujemy sobie do naszej siatki, która będzie wyglądać tak 👇:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| {Laptop} | 0 | 0 | 0 | 0 | 0 | 0 |
| {Laptop, Smartfon} | 0 | 0 | 0 | 0 | 0 | 0 |
| {Laptop, Smartfon, Konsola do gier} | 0 | 0 | 0 | 0 | 0 | 0 |
Na początku każdej komórce przypisywana jest wartość zero 0️⃣.
WIERSZ #1
Startujemy od pierwszej komórki w lewym górnym rogu - dla "podplecaka" równego 1 i dla podzbioru przedmiotów z jednym elementem ✅. Potem zadajemy proste pytanie: czy przedmiot jako jedyny w podzbiorze, zmieści się w "podplecaku" o pojemności 1 kg 🧠? Sięgamy do tabelki u góry i stwierdzamy że nie ⛔, więc zostawiamy wartość zero bez zmian 😊.
Przechodzimy do kolejnej kolumny i zadajemy to samo pytanie, natomiast już z "podplecakiem" równym 2 🫵. Dalej nie możemy umieścić laptopa, więc zostawiamy wartość zero, jak poprzednio 0️⃣.
Inna sprawa jest w przypadku "podplecaka" o 3 kilogramach, bowiem na pytanie czy można w nim zmieścić laptopa, w tym przypadku już możemy odpowiedzieć "tak" ☑️! Przypisujemy komórce wartość równą 3,000, jako wartość jedynego przedmiotu, który tym razem możemy uwzględnić 💪.
W dalszych kolumnach wystarczy zauważyć, że nie ma innych przedmiotów do wyboru w danym podzbiorze, a w każdym większym "podplecaku", tym bardziej nasz laptop się zmieści 😄! Przepisujemy te same 3,000 w całym wierszu jak leci 😇!
Oto dotychczasowe wyniki 👇:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| {Laptop} | 0 | 0 | 3000 | 3000 | 3000 | 3000 |
To są rozwiązania częściowe, czyli lokalnie optymalne rozwiązania 🌟. Na razie możemy stwierdzić tyle, że laptop da się włożyć do plecaków o pojemności większej bądź równej 3 jednostki. Ciekawi Cię co się będzie działo dalej 😉?
WIERSZ #2
Przechodzimy do następnego wiersza 2️⃣. Teraz badamy podzbiór DWUELEMENTOWY i odpowiadamy na pytanie czy do wskazanych "podplecaków", zmieści się laptop i smartfon 😯!
Sprawdzamy "podplecak" o pojemności 1 kg. Widzimy, że choć laptop nie wejdzie, to smartfon już damy radę włożyć ✅! Zapisujemy we właściwej komórce wartość smartfona (2,000) i od razu możemy zrobić to samo dla "podplecaka" o pojemności 2, bo i tutaj nie ma siły, żeby laptop się zmieścił 😅.
W kolejnej kolumnie mamy problem do rozwikłania, bowiem może zmieścić się i jeden, i drugi przedmiot, natomiast nie oba naraz ❌. Wybieramy ten, który daje największą wartość w złotówkach i okazuje się nim laptop 💻. Przepisujemy wartość bez zmian ➖.
Dla "podplecaka" o pojemności równej 4 kg, mamy rewelacyjną sytuację, bo zmieszczą się wszystkie przedmioty w rozpatrywanym podzbiorze 💪. Komórka będzie sumą obu przedmiotów (laptop + smartfon = 5,000).
Nie mamy więcej przedmiotów do zbadania, więc w całej reszcie kolumn przepisujemy to samo 😊. Rozprawiliśmy się z drugim wierszem, a tak wyglądają wyniki 👇:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| {Laptop} | 0 | 0 | 3000 | 3000 | 3000 | 3000 |
| {Laptop, Smartfon} | 2000 | 2000 | 3000 | 5000 | 5000 | 5000 |
Całkiem nieźle. Jesteśmy coraz bliżej "poznania prawdy" 😀!
WIERSZ #3
Mamy ostatni wiersz do rozpracowania i dyskretny problem plecakowy przestanie być problemem ☺️!
Dotarliśmy do ostatniego wiersza, więc teraz badamy komplet dostępnych przedmiotów (już nie fragment) 😲! Mamy zbiór trzyelementowy i stoimy na "podplecaku" o pojemności równej 1 kg.
To samo pytanie: czy którykolwiek z tych trzech przedmiotów się do niego zmieści 🤔? Tylko smartfon 📱. Nic nie ulega zmianie w całej reszcie wiersza, więc przepisujemy ✒️. Widać od razu, że jeżeli konsola do gier ma wagę 5 kg, to nie będzie żadnych innych alternatyw dla "podplecaków" o pojemności mniejszej bądź równej 4 kg 💡. Wiesz co masz robić (do czwartej kolumny) 😉.
Dla kolejnego "podplecaka" (5 kg) zadajemy sobie kluczowe pytanie: czy wartość konsoli do gier przewyższy sumę wartości laptopa i smartfona 🤯? Nie, bo 4,000 jest mniejsze od 5,000 👍! Przepisujemy wartość z poprzedniego wiersza ✏️.
A teraz ba-dum, ba-dum 🥁! Ostatnia komórka w tabeli 😯!
Pytanie: czy wartość konsoli do gier może wpłynąć na wynik 🧠? TAK!
Suma wartości konsoli do gier i smartfona przewyższy sumę wartości laptopa i smartfona, zatem tamten podzbiór jest porzucany i na jego miejsce wkracza nowy 🚀! Do komórki wpisujemy wartość 6,000 i tak oto mamy rozwiązanie końcowe 💖. Wynikiem ostatecznym jest komórka w ostatnim rzędzie i kolumnie 💥.
Oto ostateczna postać tabeli 👇:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| {Laptop} | 0 | 0 | 3000 | 3000 | 3000 | 3000 |
| {Laptop, Smartfon} | 2000 | 2000 | 3000 | 5000 | 5000 | 5000 |
| {Laptop, Smartfon, Konsola do gier} | 2000 | 2000 | 3000 | 5000 | 5000 | 6000 |
Nareszcie meta 🏁, a to tylko 3 przedmioty 😅.
Rozwiązanie otrzymane przez programowanie dynamiczne wymagało 6x3 kombinacji do zbadania, czyli iloczyn liczby przedmiotów i pojemności plecaka:
O(|I|*C) : I = zbiór przedmiotów, C = pojemność plecaka
Taka jest złożoność obliczeniowa tego podejścia 💥! To jest tzw. wzrost pseudowielomianowy. Oznacza to, że poza rozmiarem danych wejściowych, wpływ na złożoność ma jakiś dodatkowy parametr (w przypadku dyskretnego problemu plecakowego, jest nim pojemność plecaka) 🌟.
Lepiej? No pewno 😁!
KOD ŹRÓDŁOWY
Tak wygląda teoria, a teraz podsumujemy to sobie kodem źródłowym w Javie przedstawiającym dyskretny problem plecakowy rozwiązany przy pomocy programowania dynamicznego 💪. Zachęcam do eksperymentowania z danymi 😄!
KLASA "MAIN"
public class Main {
public static void main(String[] args) {
new Launcher();
}
}Jak zwykle, klasa "Main" bez zmian - tworzenie instancji, w której dzieje się cały proces algorytmiczny 🔧. I jak zwykle, zostawiamy tłumaczenie tego kawałka na koniec 🙂!
REKORD "ITEM"
public record Item(String name, int value, int weight) {
@Override
public String toString() {
return "Przedmiot: " + name + " -> {wartość: " + value + ", waga: " + weight + "}";
}
@Override
public int hashCode() {
return name.hashCode();
}
@Override
public boolean equals(Object object) {
if(getClass() != object.getClass()) {
return false;
}
var item = (Item)object;
return item.name.equalsIgnoreCase(name);
}
}Klasa danych "Item" (tworzona przy użyciu słowa "record" w języku Java) przeznaczony jest do tworzenia pojedynczego przedmiotu jaki będzie brał udział w selekcji.
Posiada 3 dane składowe (umieszczone w wierszu z nazwą rekordu) 👇:
- łańcuch znaków dla określania nazwy przedmiotu,
- liczba całkowita określająca wartość przedmiotu,
- liczba całkowita określającą tym razem wagę przedmiotu.
Więcej do szczęścia nie potrzeba 😄!
Metody jakie się tu znajdują, to są same przesłonięcia metod z klasy "Object":
- "toString", aby podczas wskazania obiektu typu "Item" do wypisania w konsoli, wyświetliły nam się informacje o tym przedmiocie, zamiast nic niemówiącego ciągu liter i cyfr 🙂,
- "hashCode" do definiowania kodu skrótu obiektu dla określenia "uznawania" dwóch obiektów za identyczne,
- "equals" z tego samego powodu, co w pkt. 2.
W języku Java, przesłonięcie "hashCode" i "equals" jest konieczne do zapewnienia, że zbiór (kolekcja nieakceptująca duplikatów) nie doda dwóch przedmiotów o tej samej nazwie 🔒. Więcej informacji na temat ustalania kryterium dla "równości" obiektów, są zawarte w załączonych artykułach ℹ️.
A propos - w Javie możesz skorzystać ze słowa "var", co pozwala pominąć pisanie typu danych danej zmiennej lokalnej 🚀!
KLASA "ITEMS"
import java. util.*;
public class Items extends HashSet<Item> {
public Items() {
add(new Item("Laptop", 3000, 3));
add(new Item("Smartfon", 2000, 1));
add(new Item("Konsola do gier", 4000, 5));
}
public Item getItemByIndexIfPossible(int index) {
Optional<Item> optionalItem = index >= 0 ? stream().skip(index).findFirst() : Optional.empty();
return optionalItem.orElse(new Item("NULL", 0, Integer.MAX_VALUE));
}
}Klasa "Items" będzie naszym zbiorem przedmiotów dostępnych do zabrania 👜.
W konstruktorze znajduje się tworzenie przedmiotów opisanych na przykładzie powyżej. Druga metoda pobiera element o podanym indeksie. Zbiór nie posiada takiej możliwości jaką dysponuje lista, więc trzeba było taką metodę zdefiniować samemu 🙂 Zapis, choć bardzo elegancki i zwięzły, może spowodować u Ciebie głowienie się nad nim 🤔, więc pozwól, że wyjaśnię o co chodzi 😉.
Ta instrukcja 👇:
index >= 0 ? stream().skip(index).findFirst() : Optional.empty();oznacza: gdy podany indeks jest większy bądź równy zero (czyli zgodność z notacją tablicową w Javie ✔️), to skonwertuj kolekcję na strumień ("stream"), pomiń N przedmiotów ("skip") i pobierz z nowego ("uciętego") strumienia pierwszy element 1️⃣. W przeciwnym razie, przypisz pustą instancję przedmiotu 🆕.
"stream" w języku Java oznacza strumień, czyli sekwencję elementów pozwalających nam na wykonanie operacji na zbiorze elementów, otrzymując nową kopię zbioru. To pozwala nam pisać w sposób funkcyjny (w roli głównej są dane, nie obiekty), w którym wykonujemy wiele czynności w jednym wierszu, tak jak u góry 👆.
"Optional" z kolei, to jest "osłona" referencji przed wartością "null" 🔥. Dzięki metodom "opakowującym" udostępnianym przez "Optional", skutecznie bronimy się przed wyjątkami "NullPointerException" zgłaszanymi w momencie próby wykonania dowolnej czynności ⛔.
Ostatecznie jednak nie zwracamy typu "Optional", tylko w razie nieznalezienia przedmiotu tworzymy "pusty przedmiot", podstawiając "śmieciowe" wartości 🧨. Ma to na celu uchronienie się przed skrajnymi przypadkami ☑️.
Tytułem wyjaśnienia dlaczego tutaj nie użyłem "var" - bo tu mamy skrajną sytuację, w której kompilator nie jest w stanie wywnioskować samodzielnie typu ℹ️
KLASA "RESULTSGRID"
public class ResultsGrid {
private final int rows;
private final int columns;
private final int[][] values;
public ResultsGrid(int rows, int columns) {
this.rows = rows;
this.columns = columns;
values = new int[this.rows][this.columns];
}
public void setValueAt(int rowIndex, int columnIndex, int value) {
if(indexesAreWithinDimensions(rowIndex, columnIndex)) {
values[rowIndex][columnIndex] = value;
}
}
public int getValueAt(int rowIndex, int columnIndex) {
return indexesAreWithinDimensions(rowIndex, columnIndex) ? values[rowIndex][columnIndex] : 0;
}
private boolean indexesAreWithinDimensions(int rowIndex, int columnIndex) {
return rowIndex >= 0 && rowIndex < rows && columnIndex >= 0 && columnIndex < columns;
}
}Ta klasa tworzy nam siatkę dla rozwiązań "podproblemów", zgodnie z opisem podejścia programowania dynamicznego 🎉.
Rezerwujemy pamięć dla 3 następujących składowych 👇:
- liczba wierszy,
- liczba kolumn,
- tablica tablic dla liczb całkowitych (czyli tablica dwuwymiarowa).
Wszystkie są finalne, co oznacza, że ich wartości nie będą mogły zostać zmodyfikowane przez cały czas istnienia tego obiektu 🔒.
W konstruktorze przypisujemy wartości do wszystkich składowych i tworzymy sobie tablicę o podanych liczbach wierszy i kolumn, tworząc tym samym tablicę 2D 😊.
Następna w kolejności metoda, odpowiada za przypisanie podanej wartości liczbowej w komórce o wskazanym wierszu i kolumnie 📝. Aby ustrzec się przed próbą wprowadzenia wartości poza wymiarami tablicy, sprawdzamy wpierw czy podany wiersz i kolumna są prawidłowe (przy użyciu osobnej metody 👌) ✅. Jeżeli tak, to podana liczba zostaje przypisana do odpowiedniej komórki i tyle 😁!
Kolejna metoda służy operacji w drugą stronę - do pobierania wartości z podanego wiersza i kolumny 😄. Najpierw badamy czy nie wyszliśmy poza ramy siatki 🔍. Jeżeli nie, "wyciągamy" wartość z odpowiedniej komórki 👍. W przeciwnym razie, przypisujemy zero 0️⃣.
A ostatnia metoda o dostępie prywatnym, która weryfikuje czy podany wiersz i kolumna nie wykraczają poza ramy naszej siatki z danymi, "siedzi" sobie na samym dole klasy 😊.
KLASA "RESULTSPRINTER"
import java. io.PrintStream;
public class ResultsPrinter {
private final PrintStream printStream = System.out;
public void printAboutInteger(int integer, String message) {
printStream.println(message + integer);
}
}Ta bardzo malutka klasa ma za zadanie tylko wypisywać komunikaty do konsoli podczas działania algorytmu, zatem możesz ją bez problemu usunąć, gdybyś jej nie potrzebował(a) 🙂.
Jedyna metoda służy do wypisywania komunikatu na temat podanej liczby całkowitej wraz z możliwością wstawienia dowolnej wiadomości tekstowej "doczepionej" do tej wartości 💬.
KLASA "LAUNCHER"
public class Launcher {
private final int knapsackCapacity = 6;
private final Items items = new Items();
private final ResultsGrid resultsGrid = new ResultsGrid(items.size() + 1, knapsackCapacity + 1);
private final ResultsPrinter resultsPrinter = new ResultsPrinter();
public Launcher() {
var highestSumOfItemsValues = getHighestSumOfItemsValues();
resultsPrinter.printAboutInteger(highestSumOfItemsValues, "Największa wartość sumaryczna: ");
}
private int getHighestSumOfItemsValues() {
var numberOfItems = items.size();
fillResultsGrid(numberOfItems);
return resultsGrid.getValueAt(numberOfItems, knapsackCapacity);
}
private void fillResultsGrid(int numberOfItems) {
for (var y = 0; y <= numberOfItems; ++y) {
for (var x = 0; x <= knapsackCapacity; ++x) {
resultsGrid.setValueAt(y, x, getValueFromCell(y, x));
}
}
}
private int getValueFromCell(int row, int column) {
if(column == 0 || row == 0) {
return 0;
}
var item = items.getItemByIndexIfPossible(row - 1);
var valueInPreviousRow = resultsGrid.getValueAt(row - 1, column);
var valueWithAddedItem = getValueFromCellDependingOnFitnessInKnapsack(row, column, item);
return Math.max(valueInPreviousRow, valueWithAddedItem);
}
private int getValueFromCellDependingOnFitnessInKnapsack(int row, int column, Item item) {
var itemWeight = item.weight();
var itemFitsInKnapsack = itemWeight <= column;
return itemFitsInKnapsack ? item.value() + resultsGrid.getValueAt(row - 1, column - itemWeight) : 0;
}
}Tak oto została nam najważniejsza klasa do wyjaśnienia 😅.
U góry mamy 4 dane składowe 👇:
- liczbę całkowitą do określenia pojemności plecaka,
- obiekt z listą przedmiotów branych pod uwagę,
- obiekt siatki dla notowania rozwiązań "podproblemów" (i wyznaczenia rozwiązania ostatecznego),
- obiekt do wypisywania komunikatów (który możesz usunąć, jak nie jest Ci potrzebny 😉).
Ponieważ nie planujemy przypisywania nowych wartości (albo referencji) do żadnej z tych zmiennych, możemy wstawić modyfikator "final" 🔥.
Aby nasz algorytm wykorzystujący programowanie dynamiczne wypalił, musimy podejść niekonwencjonalnie do wymiarów siatki ⚠️. Ze względu na notację indeksową w języku Java, w której elementy liczy się od zera, o wiele lepiej jest przesunąć się ze wszystkimi wartościami o jeden rząd i kolumnę do przodu, stąd mamy "plus jeden" do rzędów i kolumn ℹ️.
Konstruktor składa się tylko z dwóch instrukcji:
- zdefiniowanie zmiennej do wyznaczenia najwyższej wartości sumarycznej wszystkich uwzględnionych przedmiotów (za wartość, przypisujemy wywołanie metody uruchamiającej algorytm 💪),
- wywołanie metody wypisującej komunikat o uzyskanej liczbie całkowitej.
Dyskretny problem plecakowy jest rozwiązywany w kolejnej metodzie (idąc od góry) 🙂! Najpierw pobieramy liczbę przedmiotów do rozpatrzenia 📱, potem wywołujemy kolejną metodę "wypełniającą" komórki naszej siatki danymi cyfrowymi (następna w kolejności) 🔢, a na wyjściu zwracamy wynik w postaci ostatniego wiersza i ostatniej kolumny, czyli największa wartość sumaryczna 📈! To jest miejsce zakończenia działania naszego algorytmu 🏁! Natomiast nie koniec tłumaczenia całej reszty, zatem idźmy dalej 😁!
W następnej metodzie wykonuje się "wypełnianie" naszej siatki wynikami rozwiązań "podproblemów". Otwieramy pętlę "for", która będzie odpowiadać za przemieszczanie się po wierszach (oś Y), a w niej otwieramy drugą pętlę "for" iterującą tym razem po kolumnach (oś X). W środku tychże pętli wywołujemy sobie metodę przypisującą wartość w danym wierszu i kolumnie, którą pozyskujemy z kolejnej metody 🚀.
Teraz sam proces wyznaczania wartości dla danej kratki 💎. W tej metodzie, musimy najpierw sprawdzić czy przypadkiem nie "stoimy" na pierwszym rzędzie bądź kolumnie (indeksy równe zero). Ma to na celu zabezpieczyć program przed próbą operowania na indeksach wykraczających poza rozmiar naszej siatki 🔒, bo później są przeprowadzane przesunięcia w kratkach ⚠️. Jeżeli w którejś z osi znajduje się wartość zero, to znak, że "poruszamy się" po "zerowym" podzbiorze przedmiotów bądź próbujemy coś wepchnąć do "zerowego podplecaka" 0️⃣. Oba te przypadki są bez sensu, zatem wtedy metoda ma zwrócić wartość zero ❌. Jeżeli tak nie jest, to przystępujemy do wyznaczenia wartości ✊!
Pierwszym punktem, jest pobranie przedmiotu o odpowiednim indeksie (podzbiór przedmiotów) korzystając z metody zawartej w klasie dla listy przedmiotów 💻. Następnie, pobieramy wartość z poprzedniego wiersza naszej siatki (zaraz się dowiesz dlaczego). Ostatnim krokiem jest wyliczenie przez następną metodę w klasie (pierwszą od dołu) wartości jaką posiadałaby dana komórka, gdyby uwzględniono kolejny przedmiot (tłumaczę w dalszej części jak to się odbywa ℹ️)🔴! A na samym końcu mamy zwrócenie na wyjściu większej z dwóch wartości, czyli:
- wartość obecnie zanotowana w poprzednim wierszu,
- wartość hipotetyczna w przypadku uwzględnienia badanego przedmiotu (biorąc pod uwagę opłacalność i możliwość).
Przed nami ostatnia metoda do wytłumaczenia 🔥🔥🔥!!! Ona ma za zadanie ustalić czy dany przedmiot, przy obecnie rozpatrywanym podzbiorze przedmiotów i pojemności "podplecaka", zmieści się w nim ✅.
Tworzymy sobie dwie zmienne lokalne:
- wartość wagi przedmiotu,
- wynik sprawdzenia czy przedmiot może się zmieścić w "podplecaku".
Na końcu zwracamy wartość liczbową i to chyba jest najbardziej zagadkowa instrukcja do zrozumienia 🧠
To chyba najbardziej skomplikowana instrukcja do zrozumienia. Operator trójargumentowy, jaki tu został wstawiony, definiuje nam 2 przypadki w zależności od tego, czy przedmiot może być włożony do plecaka ✔️, czy nie ❌.
Jeżeli przedmiot można włożyć do "podplecaka", to wyznaczamy wyrażenie w postaci sumy wartości przedmiotu i uprzednio zanotowanej wartości w siatce z poprzedniego wiersza "cofniętej" o liczbę kolumn równej wadze tego przedmiotu 😅. To przesunięcie w kolumnach oznacza "powrót" do momentu wybrania przedmiotu w poprzednim rzędzie i "zamianę" na przedmiot o większej wartości, który na pewno zmieści się w aktualnym (większym) "podplecaku". Jaśniej już nie mogę tego wyjaśnić 😜!
Jeżeli przedmiotu nie da się włożyć do "podplecaka", to po prostu zwracamy wartość zero 0️⃣. Ponieważ mamy wywołanie "Math.max" w poprzedniej metodzie, spowoduje to wtedy, że zostanie przepisana wartość komórki z poprzedniego rzędu, co zostanie uznane za najwyższy możliwy wynik (bo dowolna wartość większa od zera, zawsze będzie większa od zera 😄).
I to koniec tłumaczenia 😊! Jest kilka ciekawych sposobów na wykorzystanie tego algorytmu w praktyce 🎯. Na przykład możesz się zapytać algorytmu za co się wziąć w pierwszej kolejności z zadań do wykonania. Wtedy, za pojemność plecaka podstawiasz liczbę dni jakie Ci zostały, a "przedmiotami" będą zadania z określonym priorytetem (jako "wartość") oraz ile dni czasu przewidujesz na jego wykonanie (jako "waga") 💡.
To wszystkie informacje jakie chciałem Ci przekazać na ten temat 😊. Ruszaj przez życie z nowo zdobytą wiedzą 🚀!