Przeszukiwanie wszerz. Teoria i kod źródłowy

W dzisiejszym materiale przynoszę na tacy wytłumaczenie algorytmu (razem z kodem 😉) jakim jest przeszukiwanie wszerz 🔍. Temat dotyczy wyszukiwania danego elementu przy jak najmniejszej liczbie iteracji, więc powinien wzbudzać zainteresowanie wśród początkujących, jako że stanowi pierwszy krok do zagadnienia wyznaczenia najkrótszej ścieżki w grafie 😱! Wszystko wytłumaczę punkt po punkcie jak należy się z tym obchodzić i jak rozumieć działanie, a więc rozpoczynajmy 🚀!

PRZESZUKIWANIE WSZERZ ZNAJDZIE CI SZUKANY ELEMENT W GRAFIE!

Zanim przejdziemy do samego problemu algorytmicznego, muszę uświadomić Ci czym w matematyce jest graf, ponieważ na nim będziemy bazować podczas opisywania tematu ℹ️.

CZYM JEST GRAF?

Graf jest strukturą danych, która ukazuje powiązania (relacje) między różnymi obiektami 🔌. 2 terminy jakie trzeba znać i nie ma od nich ucieczki jeśli chodzi o grafy, to 👇:

1. węzeł (bądź wierzchołek),
2. krawędź.

Węzeł (wierzchołek) jest to obiekt, który może wchodzić w relacje z innymi obiektami (określa się ich wtedy "sąsiadami"). Ponieważ jest to struktura abstrakcyjna, kontekst czy też interpretacja czym jest węzeł, zależy od zastosowania ⚠️.

Przykładowo, graf reprezentujący sieć grona znajomych na Facebooku będzie składać się z węzłów rozumianych jako samych znajomych 👪. Z kolei gdy mamy graf w postaci sieci informatycznej, to węzłami będą routery albo punktu dostępu (ang. access points) i tak dalej 🙂.

Węzeł może połączyć się z każdym innym węzłem i tak przechodzimy do drugiego terminu, jakim jest krawędź 💡. Krawędź jest właśnie tym połączeniem od jednego węzła do drugiego, który oznacza, że między tymi węzłami zachodzi relacja. I znowu, znaczenie połączeń zależy od postawionego problemu 😄.

Połączenia między znajomymi na Facebooku będą oznaczały, że dane osoby znane są sobie (przynajmniej internetowo) 🤝. A jak przyjrzymy się sieci informatycznej, to połączenie routerów ze sobą oznaczać będzie, że jest dostępne przejście od jednego do drugiego 🌐.

Jak widzisz, może to być bardzo urozmaicone 😊.

Na ten moment nie musisz nic więcej wiedzieć o grafach, tak więc wróćmy do tematu, jakim jest przeszukiwanie wszerz ↩️ !

DZIAŁANIE PRZESZUKIWANIA WSZERZ

Przeszukiwanie wszerz (ang. breadth-first search) rozwiązuje problem należący do kategorii wyszukiwania najkrótszej ścieżki (ang. shortest path problem). Innymi słowy, pozwala na wyznaczanie ścieżki znane bardziej jako "pathfinding" 🤩!

Dysponując dowolnym grafem, algorytm jest w stanie go "przeszukać" w poszukiwaniu wskazanego przez Ciebie węzła, tym samym odpowiadając na 2 pytania 👇:

1. czy istnieje droga z węzła startowego do węzła docelowego?
2. jaka jest droga z węzła startowego do węzła docelowego (jeśli punkt pierwszy jest spełniony)?

Może nas interesować sama odpowiedź w postaci "decyzyjnej" (punkt 1), natomiast dużo częściej pożądane jest opracowanie całej ścieżki od punktu A do punktu B ➡️.

Rozpatrzmy sobie jakiś przykład 👀. Mamy taki oto graf 👇:

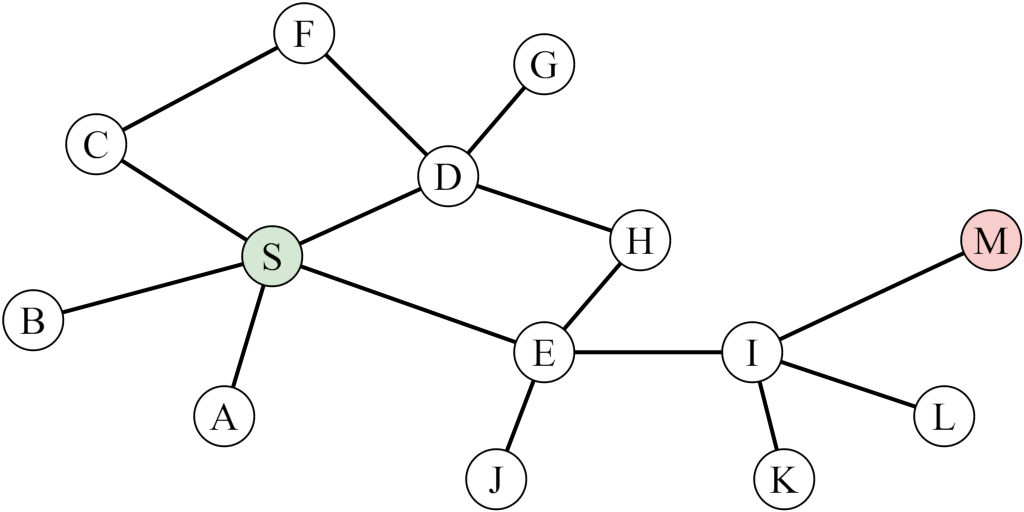Rysunek graficzny prezentujący graf nieskierowany.

i interesuje nas odnalezienie punktu oznaczonego kolorem czerwonym (M) rozpoczynając od punktu startowego o kolorze zielonym (S). Zatem, mamy klasyczny problem ustalenia jaka (i czy w ogóle) istnieje ścieżka od jednego węzła do drugiego 🤔.

Problem: odnalezienie wskazanego węzła w grafie na podstawie podanego kryterium

Pierwszym krokiem jest pobranie oraz usunięcie ze zbioru węzła początkowego i sprawdzenie jego właściwości (np. długości nazwy) czy przypadkiem on sam nie jest przez nas poszukiwanym 😊.

Jeżeli nie, to dodaje do zbioru węzłów wszystkich jego sąsiadów, a sam węzeł oznacza jako "odwiedzony" lub "zbadany" (to jest cholernie ważne i zapobiega zapętleniu się programu w nieskończoność 💥!). Ten sam ciąg instrukcji powtarza się dopóty, dopóki nie zostanie odnaleziony element, o który nam chodzi (bądź nie opróżni się lista pozostałych węzłów do sprawdzenia ℹ️) 🔁.

"PIERWSZY WCHODZI, PIERWSZY WYCHODZI"

W przypadku przeszukiwania wszerz, kolejność dodawanych nowych węzłów odgrywa kolosalną rolę ⚠️! Nowe elementy muszą być dodawane na sam koniec listy, za każdym razem gdy algorytm "stwierdzi", że to nie ten którego szukamy ❌.

To działa tak, jakbyśmy szukali pracy (dla przykładu) 🔍. Najpierw staramy się samodzielnie. Kiedy nie dajemy sobie rady, prosimy o pomoc najbliższych znajomych 📣. Jeżeli to nie przynosi rezultatu, sięgamy do znajomych znajomych i tak dalej 📰. Wtedy jest gwarancja, że program będzie działał zgodnie z oczekiwaniami ✔️.

Wniosek jest prosty: żeby algorytm działał prawidłowo, musi być zachowana odpowiednia kolejność "przepytywania" poszczególnych węzłów ‼️. Pisząc krótko, "wchodzi" zawsze pierwszy, a na końcu dodawani są sąsiedzi i mają być zawsze umieszczeni na samym końcu!

Sposób przeprowadzania operacji w podanej kolejności doczekało się słynnego terminu: "Last In, First Out" (w skrócie "LIFO"), a strukturą danych w takim przypadku jest kolejka 🔥. Kolejkę wyróżnia możliwość "wyciągania" elementów tylko z jej początku, a nowe elementy pojawiają się zawsze na końcu (tak jak w prawdziwej kolejce po mięso za komuny 😁).

PRZESZUKIWANIE WSZERZ MA SWOJE "ALE"

Jak wszystko inne w dziedzinie informatycznej, ten algorytm też ma swoją wadę ⛔. Jest nią brak rozróżniania "wagi" (czy też "jakości") dostępnych węzłów, po jakich można "przejść". On nie weźmie pod uwagę, że mogą istnieć inne, lepsze ścieżki od punktu A do B i wszystkie węzły traktuje na równi - po prostu weźmie pierwszą dostępną ścieżkę i taką zwróci.

Jeżeli zależy Ci na wyznaczaniu ścieżki w wyznaczonym grafie, uwzględniając wagi poszczególnych węzłów, które mogłyby na ten przykład symulować jakiś trudny teren (węzły po których można przejść, tylko jest to bardziej kosztowne, niż u innych), to tu przeszukiwanie wszerz odpada i trzeba sięgnąć choćby po bardzo popularny algorytm Dijkstry, który już potrafi wyznaczać ścieżki na grafach ważonych ⭐.

JAKA ZŁOŻONOŚĆ CZASOWA?

No to mamy wyjaśnione co to za algorytm, jak podchodzi do grafu i co potrafi 👍. A teraz zastanówmy się jaka jest efektywność od strony czasu ⌚. W najgorszym przypadku (według notacji dużego O), będzie następująca 👇:

O(|V| + |E|) : V = zbiór węzłów, E = zbiór krawędzi

Suma mocy zbioru węzłów i zbioru krawędzi, czyli inaczej: suma wszystkich węzłów i krawędzi jakie występują w grafie ✅.

W najgorszym przypadku, przeszukiwanie wszerz musi przeczesać wszystkie węzły w podanym grafie w poszukiwaniu wskazanego węzła 🔍. Mamy sumę, ponieważ za każdym razem, jeżeli badany element nie jest tym, który nas interesuje, dodajemy do zbioru wszystkie pozostałe węzły będące w bezpośrednim sąsiedztwie z już zweryfikowanym wierzchołkiem ℹ️.

KOD ŹRÓDŁOWY

Tym sposobem, docieramy do praktyki 🎯! Raz kolejny częstuję Cię kodem źródłowym w języku Java, aby wyjaśnienie materiału było zapięte na ostatni guzik ⏏️!

KLASA "MAIN"

public class Main {
	public static void main(String[] args) {
		new Launcher();
	}
}

Tradycyjnie, wszystko się zaczyna od klasy uruchamiającej cały program ▶️. Tworzymy instancję klasy, w której znajduje się algorytm przeszukiwania wszerz 🔧. Tę klasę opiszemy sobie na samym końcu 😉.

KLASA "NODE"

import java. util.LinkedHashSet;

public class Node {
	private final String name;
	private final LinkedHashSet neighbours = new LinkedHashSet<>();
	
	private boolean isVisited;
	
	@Override
	public int hashCode() {
		return name.hashCode();
	}
	
	@Override
	public boolean equals(Object object) {
		if(getClass() != object.getClass()) {
			return false;
		}
		
		var node = (Node)object;
		
		return getName().equals(node.getName());
	}
	
	public Node(String name) {
		this.name = name;
	}
	
	public void addNodeAsNeighbour(Node node) {
		if(node != null) {
			neighbours.add(node);
		}
	}
	
	public void setAsVisited() {
		this.isVisited = true;
	}

	public String getName() {
		return name;
	}
	
	public LinkedHashSet getNeighbours() {
		return neighbours;
	}
	
	public boolean isVisited() {
		return isVisited;
	}
}

Tu mamy klasę do tworzenia węzłów w grafie 🔵. Tutaj mamy nieco więcej kodu, dlatego wytłumaczę wszystko po kolei 💡.

Dwie składowe z modyfikatorem "final", oznaczają następujące dane 👇:

1. nazwa węzła (czy jego etykieta),
2. lista węzłów sąsiednich ("LinkedHashSet").

Tutaj, dla przechowywania listy sąsiadów, korzystam z typu "LinkedHashSet" 🔥. "HashSet" to struktura danych typu zbiór, dzięki której nie dojdzie do sytuacji, że ten sam węzeł zostanie dodany 2 razy 👍. Aby zapewnić, że do tego nie dojdzie, w Javie jest taki zwyczaj, że trzeba odpowiednio przesłonić 2 metody występujące w klasie "Object":

1. hashCode,
2. equals.

To ma związek z klasyfikacją identyczności obiektów - ten wątek opisałem w osobnych artykułach z cyklu języka Java ☕. Przedrostek "Linked", oznacza zdolność listy do zapamiętywania kolejności dodawanych elementów, które jest niezbędne do zapewnienia prawidłowego działania ✅!

Ostatnia ze składowych to jest "boolean", do późniejszego oznaczania węzłów jako "odwiedzone" 🚩. Tu wyjątkowo nie możemy nałożyć modyfikatora "final", ponieważ wartość tej zmiennej będzie musiała ulec zmianie podczas działania programu ℹ️.

Teraz metody (zaraz po "hashCode" i "equals"):

• konstruktor służy do przypisywania nazwy węzłowi,
• "addNodeAsNeighbour" dodaje wskazany węzeł do listy sąsiadów (zabezpieczamy się przed wartością "null" odpowiednią instrukcją warunkową),
• "setAsVisited" oznacza nasz węzeł jako "odwiedzony",
• "getName" pobiera nazwę węzła,
• "getNeighbours" pobiera listę sąsiadów danego węzła,
• "isVisited" pobiera "status" naszego węzła (odwiedzony/nieodwiedzony).

Ostatnich parę słów o słowie kluczowym "var" - dzięki niemu, możesz pominąć wstawianie typu danych zmiennej lokalnej ℹ️. Bardzo przydatna rzecz 👍!

KLASA "GRAPH"

import java. util.LinkedHashSet;

public class Graph {
	private final LinkedHashSet<Node> nodes = new LinkedHashSet<>();
	
	public Graph() {
		var nodeA = new Node("Magnes");
		var nodeB = new Node("Foremka");
		var nodeC = new Node("Bibuła");

		nodes.add(nodeA);
		nodes.add(nodeB);
		nodes.add(nodeC);

		nodeB.addNodeAsNeighbour(nodeA);
		nodeC.addNodeAsNeighbour(nodeA);
	}

	public LinkedHashSet<Node> getNodes() {
		return nodes;
	}
}

Kolejna osobna klasa, tym razem do tworzenia całego grafu (razem z połączeniami). Tutaj zrobiłem bardzo prosty przykład, on nie przedstawia tej samej postaci, co rysunek u góry, ponieważ wyszłoby bardzo dużo podobnych instrukcji, które odciągałyby od reszty kodu ℹ️.

U góry tworzymy sobie listę węzłów jakie mają wchodzić w strukturę grafu 🔌. W konstruktorze znajduje się tworzenie samych węzłów i połączeń między nimi 💪. Tworzymy sobie 3 węzły, nadajemy im nazwy, a następnie dodajemy je do listy typu również "LinkedHashSet" ☑️.

Metoda na samym dole, zwraca naszą sieć węzłów i to wszystko na temat 😀!

KLASA "NODESQUEUE"

import java. util.LinkedHashSet;

public class NodesQueue extends LinkedHashSet<Node> {
	public Node popFirst() {
		if(isEmpty()) {
			return null;
		}

		var node = getFirst();

		remove(node);

		return node;
	}

	public void addNeighboursOf(Node node) {
		if(node != null) {
			addAll(node.getNeighbours());
		}
	}
}

A tu mamy naszą kolejkę do dodawania i usuwania węzłów do przeanalizowania 🌐. Dziedziczymy sobie od "LinkedHashSet", aby móc skorzystać z uprzednio zdefiniowanych metod do operowania na elementach tego zbioru 👍.

Wyjaśniam resztę metod 👇:

• "popFirst" służy do zwracania pierwszego węzła w liście "ala kolejce" i jednocześnie usuwa go z listy (jeżeli nie ma żadnego węzła w grafie, to zwracamy wartość "null", aby nie doprowadzić do zgłoszenia wyjątku),
• "addNeighboursOf" dodaje wszystkie węzły sąsiednie podanego w parametrze węzła do grafu.

"popFirst" symuluje to, co znajdziesz w wielu językach programowania i w strukturach danych typu "lista" (tablica też w niektórych językach, choć to nie leży w naturze tej struktury danych). Mianowicie, zwraca pierwszy w kolejności element (metoda "getFirst"), przypisuje referencję, a zaraz potem go usuwa ze zbioru i jednocześnie zwraca na wyjściu. Zbiór nie posiada takiej funkcjonalności, więc trzeba było taką metodę zdefiniować osobno 🙂.

I to tyle 😄!

KLASA "RESULTSPRINTER"

import java. io.PrintStream;
import java. util.function.Function;

public class ResultsPrinter {
	private final PrintStream printStream = System.out;

	public void printAboutNode(Node node, Function<Node, String> function, String message) {
		if(node != null && function != null) {
			printStream.println(message + function.apply(node));
		}
	}
}

Ostatnia klasa poza tą "główną" służy jedynie do wypisywania komunikatów w konsoli na temat wskazanego węzła ℹ️. Tutaj korzystam z interfejsu funkcyjnego "Function", które pozwala mi wstawić dowolne wyrażenie pochodzące od klasy węzła, zwracające na wyjściu łańcuch znaków. Więcej informacji, w załączonym artykule 👈.

KLASA "LAUNCHER"

public class Launcher {
	private final Graph graph = new Graph();
	private final NodesQueue nodesQueue = new NodesQueue();
	private final ResultsPrinter resultsPrinter = new ResultsPrinter();
	
	private Node searchedNode;
	
	public Launcher() {
		nodesQueue.addAll(graph.getNodes());
		attemptToFindSearchedNode();
		resultsPrinter.printAboutNode(searchedNode, Node::getName, "Znaleziono szukany węzeł o nazwie: ");
	}
	
	private void attemptToFindSearchedNode() {
		while (!nodesQueue.isEmpty() && searchedNode == null) {
			handleNextNodeInOrder();
		}
	}

	private void handleNextNodeInOrder() {
		var currentNode = nodesQueue.popFirst();

		resultsPrinter.printAboutNode(currentNode, Node::getName, "Obecny węzeł: ");
		handleNodeIfNeeded(currentNode);
	}

	private void handleNodeIfNeeded(Node node) {
		if(node == null || node.isVisited()) {
			return;
		}

		if(isSearchedNode(node)) {
			searchedNode = node;
		} else {
			onNeighbouringNodesNeedToBeAdded(node);
		}
	}

	private boolean isSearchedNode(Node node) {
		return node != null && node.getName().length() == 7;
	}

	private void onNeighbouringNodesNeedToBeAdded(Node node) {
		if(node == null) {
			return;
		}

		node.setAsVisited();
		nodesQueue.addNeighboursOf(node);
	}
}

Jesteśmy przy klasie, której obiekt tworzy się na samym początku 😊. Lećmy od góry 🚀!

Mamy 4 składowe - 3 z nich są finalne, czyli nie będą zmieniać swojej referencji w czasie działania 👇:

1. obiekt grafu,
2. obiekt kolejki,
3. obiekt do wypisywania komunikatów,
4. referencja do szukanego węzła (początkowo przyjmuje wartość "null" - ponieważ może zmienić swoją wartość, tu wyjątkowo nie można wstawić modyfikatora "final").

Niżej mamy konstruktor stanowiący "zapalnik" przeszukiwania wszerz 🔥. Najpierw wywołujemy metodę dodającą wszystkie węzły do zbadania z grafu do kolejki, aby miała początkowe dane do rozpoczęcia działania 📀. Potem jest wywołanie metody do rozpoczęcia przeszukiwania grafu i na końcu, wypisywanie komunikatu o znalezionym węźle (jeśli faktycznie został odnaleziony 🙂).

Tak przechodzimy do samego algorytmu. Przeszukiwanie wszerz musi wykonywać się w pętli "while", ponieważ my nie wiemy ile węzłów będziemy musieli zbadać, aby odnaleźć ten, którego szukamy ℹ️. Proces szukania powtarzamy tak długo, aż wydarzy się jeden z 2 przypadków:

1. węzeł zostanie znaleziony,
2. lista węzłów do zbadania się wyczerpie.

Jeżeli przeszukiwanie wszerz nie dobiegło końca, to przechodzimy do kolejnej metody, w której pobieramy (i usuwamy!) pierwszy węzeł z kolejki. Po wypisaniu kolejnego komunikatu, przechodzimy do kolejnej metody, w której algorytm ma za zadanie "obsłużyć" aktualnie badany węzeł 🔍.

Najpierw sprawdzamy czy węzeł w ogóle istnieje (różny od "null"). Zaraz potem, czy nie został zbadany wcześniej ✅. Po upewnieniu się, że węzeł istnieje i nie został "odwiedzony", algorytm wchodzi do metody i sprawdza czy to jest ten element, którego szukamy ❓. Uzależniamy wynik od kolejnej metody wywoływanej wewnątrz instrukcji warunkowej.

W tym przykładzie, kryterium polega na tym, czy nazwa węzła składa się dokładnie z 7 znaków 😁. To jest bardzo trywialne, jednak nie chciałem komplikować całego kodu, który już w chwili obecnej jest całkiem sporych rozmiarów 💪. Zawsze możesz do węzła wprowadzić jakąś składową (np. liczbę) i z tej wartości zrobić kryterium do wyszukiwania danego elementu ℹ️.

Zależnie od rezultatu, może stać się jedna z 2 rzeczy:

1. jeżeli to ten węzeł spełnia nasze wymaganie, to program przypisuje jego referencję do instancji węzła (określanego jako "znaleziony poszukiwany") i przerywa dalsze działanie pętli uznając poszukiwania zakończone sukcesem ✅,
2. jeżeli dany węzeł nie jest tym, którego szukamy, to wywołuje się odrębna metoda wykonująca 2 ważne instrukcje:
   1. zmienia stan zbadanego węzła na "odwiedzony",
   2. dodaje do kolejki wszystkie węzły sąsiednie.

I to wszystko! Na samym końcu, jeżeli udało się znaleźć węzeł, to jest wypisywany stosowny komunikat 💬.

Mamy następny wyjaśniony algorytm tak dokładnie, jak tylko byłem w stanie 😉! Miłego studiowania 📖!

PODOBNE ARTYKUŁY

• Sortowanie szybkie. Teoria i kod źródłowy
• Dziel i zwyciężaj w algorytmice. Metoda "dzielenia problemu"
• Sortowanie przez wybieranie. Teoria i kod źródłowy