"Dziel i zwyciężaj", to jeden z kolejnych ważnych tematów w algorytmice, jaki teraz weźmiemy sobie pod lupę 🔍. Termin jest jedną z metod projektowania algorytmu, więc temat dla Ciebie jest obowiązkowy do przeczytania 👀!
"DZIEL I ZWYCIĘŻAJ". W ROLI GŁÓWNEJ, DZIELENIE PROBLEMU NA MAŁE CZĘŚCI!
Poznasz teraz jedną z technik postępowania z danym problemem algorytmicznym 😮. "Dziel i zwyciężaj" (ang. divide and conquer), to metoda rozwiązywania postawionego problemu poprzez dzielenie go na mniejsze kawałeczki ("podproblemy"), aby krok po kroku dojść do ostatecznego rozwiązania ✅. Polega na wykonaniu 3 kroków 👇:
- podzieleniu problemu na mniejsze podproblemy,
- rozwiązaniu podproblemów,
- "sklejeniu" (złączeniu) wszystkich rozwiązań podproblemów w jedną całość, tym samym uzyskując rozwiązanie całego problemu.
To tak w największym skrócie o co "come on" w tym terminie 😊.
PRZYPADEK PODSTAWOWY I REKURENCYJNY
Istotną cechą algorytmów korzystających z techniki "dziel i zwyciężaj", jest rekurencyjne rozwiązywanie "po kawałku", aż do dojścia do tzw. "przypadku podstawowego" - to jest moment "łączenia" wszystkich otrzymanych wyników podproblemów w jedną całość 🧩. Rekurencja jest kolejnym arcyważnym terminem w nauce informatycznej, który oznacza odwoływanie się funkcji do samej siebie (więcej informacji znajdziesz w załączonym artykule) ℹ️.
Działanie algorytmu w oparciu o "dziel i zwyciężaj", z punktu widzenia kodu, dzieli się na 2 części 👇:
- przypadek rekurencyjny (dzielenie problemu na mniejsze podproblemy),
- przypadek podstawowy (moment "łączenia" wyników w jedną całość).
Przypadek podstawowy to moment, w którym następuje przerwanie rekursywnego "dzielenia" problemu ✂️. Innymi słowy, jest to sytuacja, w której pętla nie wykonuje dalej przekazanych instrukcji ℹ️.
Przypadek rekurencyjny, to zapętlone wykonywanie instrukcji mających na celu "ćwiartowanie" problemu na coraz mniejsze części, aż do spełnienia określonego warunku np. osiągnięto dostateczny próg błędu, licznik iteracji doszedł do zadanej wartości i tak dalej. "Kodowo" rzecz ujmując, to jest instrukcja warunkowa, która stanowi "granicę" pomiędzy przypadkiem podstawowym, a rekurencyjnym 🚧. Przypadek rekurencyjny zachodzi w momencie wejścia do ciała instrukcji warunkowej po spełnieniu warunku.
Należy uważać przy programowaniu podejściem "dziel i rządź" ze względu na naturę działania rekurencji ⛔! Kiedy nie uwzględnimy sprowadzenia do przypadku podstawowego, to grozi nam działanie programu w kółko, aż do pięknego powiadomienia o przepełnieniu stosu 😏.
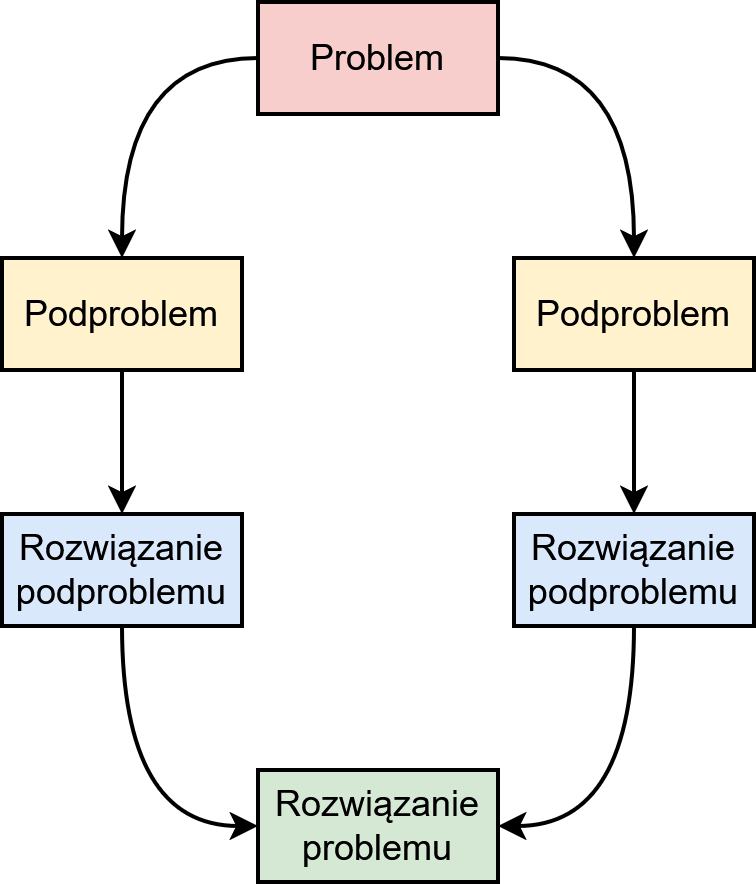 |
"Dziel i zwyciężaj" to technika "ćwiartująca" dany problem na mniejsze części używając (zwykle) rekurencyjnych wywołań metody.
REKURENCJA NIE MUSI KONIECZNIE WYSTĘPOWAĆ
Pragnę w tym miejscu zaznaczyć, że choć metoda "dziel i zwyciężaj" opiera się głównie na rekurencji, to nie jest powiedziane, że jeżeli algorytm został napisany w sposób iteracyjny (z użyciem pętli "while"), to już nie korzysta z tej techniki ⚠️. Korzystając z pętli także możesz "podzielić problem" 🙂. Tylko wtedy ten proces nie jest aż tak "widoczny" w kodzie, bo podczas gdy rekurencja opiera się na rosnącym stosie wywołań, tak pętla "gromadzi" zmiany w utworzonej zmiennej, która jest stale aktualizowana ✔️.
PRZYKŁADY ALGORYTMÓW OPIERAJĄCYCH SIĘ O METODĘ "DZIEL I ZWYCIĘŻAJ"
Tu masz kilka przykładów algorytmów, które opierają się na strategii "dziel i zwyciężaj" 👇:
- wyszukiwanie binarne,
- sortowanie szybkie,
- sortowanie przez scalanie.
Wszystkie wyżej wymienione przykłady charakteryzuje jeden szczegół: dzielenie problemu co iterację 🔥.
W ramach lepszego zrozumienia zasady działania "dziel i zwyciężaj", polecam wziąć sobie jakiś przykład algorytmu i porównać sobie postać iteracyjną oraz rekurencyjną, tak aby obie mieć je na widoku 👀. Jak dostrzeżesz to "ćwiartowanie" problemu na mniejsze kawałki przy pomocy rekurencji, to zrozumiesz "clue" tej techniki 🧠.
I to wszystko na dziś 😄! Radzę dobrze zrozumieć ten temat - to jeden z kluczowych w algorytmice ‼️.