Czas na pierwszy merytoryczny materiał na temat algorytmów 🔧! Na wstęp, przygotowałem wyjaśnienie czym jest algorytm 🔢. Definicja wraz z dawką najistotniejszych informacji powinna wystarczyć, aby Cię oswobodzić z więzów niewiedzy na ten temat 😜!
ALGORYTM TWOIM REMEDIUM NA DANY PROBLEM!
Definicja jest następująca: algorytm to zestaw poszczególnych instrukcji mających za zadanie rozwiązanie postawionego problemu, przy czym ważna jest kolejność ich wykonywania, bo musi zgadzać się w 100% z podaną "recepturą" 📜.
Jest to nic innego jak postępowanie krok po kroku co należy robić i z czym, aby osiągnąć zamierzony cel 🎯, dysponując pewnymi danymi wejściowymi. Częstym przykładem podawanym w literaturze jest przepis na wykonanie jakiegoś dobrego dania czy deseru 🧁. Tam też masz instrukcję krok po kroku co należy robić, jakie składniki są potrzebne i jak postępować, aby otrzymać taki efekt końcowy, jaki został napisany. Nie inaczej jest tutaj ✅.
Ponumerowana lista czynności jest algorytmem. Dane wejściowe, to składniki do ciasta czy innej potrawy (ile gramów). W obu przypadkach trzeba trzymać się kolejności, aby nie popsuć całej pracy 🙂. Tak samo działa algorytm w informatyce. Może "prawie" tak samo, bo nie trzeba kupować niczego w sklepie, a komputery nie brudzą na stole 😁.
"JĘZYK" ALGORYTMÓW
Definicję mamy za sobą. Teraz sposoby utrwalania dowolnego algorytmu 📝. Są 3 metody zapisu przebiegu algorytmu 👇:
- pseudokod (lista),
- schemat blokowy (grafika),
- kod źródłowy (rozumiane samo przez się 😉).
Należy bezsprzecznie wiedzieć jak możesz zapisać algorytm na potem, więc poznaj te 3 metody czym się różnią między sobą 3️⃣!
We wszystkich 3 zapisach, będę opierał się na tym samym programie wypisującym aktualny licznik iteracji od 1 do 100 ℹ️.
PSEUDOKOD
Słyszałeś(-aś) o "pseudokodzie" 🙂? Jest to lista czynności zapisanych językiem naturalnym, które mają zostać wykonane w podanej kolejności. Przykład takiego pseudokodu wygląda następująco 👇:
- zainicjuj zmienną i = 1,
- dopóki zmienna i jest mniejsza bądź równa od 100:
- wypisz i,
- inkrementuj i,
- wróć do pkt. 2.
Dokładnie tak, jakbyś czytał(a) przepis z książki kucharskiej 📖. Może za wyjątkiem "powracania" do poprzednich kroków, bo w gastronomii nie ma pętli 😄.
SCHEMAT BLOKOWY
Schemat blokowy to druga postać przedstawiająca przebieg postępowania działania określonego algorytmu, tylko już w sposób graficzny 🎨. Zapis wciąż ma wyglądać na prosty i abstrakcyjny, jednak prezentacja obrazkowa mówi nam już dużo więcej o samym przebiegu algorytmu. Widać jednak, że jest już nieco bardziej złożona i wymaga przestrzegania paru zasad notacji ℹ️.
Tak wygląda przykładowy schemat blokowy odpowiadający algorytmowi zapisanemu powyżej 👇:
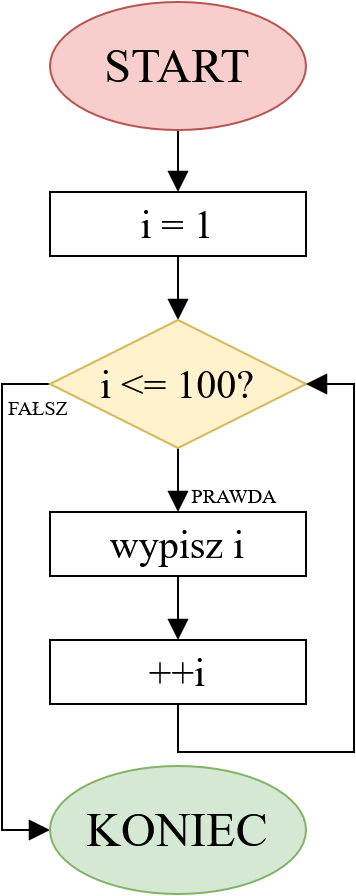 |
Schemat blokowy algorytmu programu wypisującego liczby od 1 do 100.
Wszystko zaczyna się od punktu "START" 🆕. Strzałki wskazują na przebieg kolejnych wykonywanych po sobie instrukcji. Prostokąty oznaczają instrukcje przypisania bądź dowolnej operacji arytmetycznej przeprowadzonej na danej zmiennej. Romb jest warunkiem decyzyjnym mającym wpływ na tzw. przepływ programu, czyli w którą stronę program pójdzie dalszym torem (odpowiednik instrukcji warunkowej ✔️). Kiedy dojdzie do punktu opatrzonego tekstem "KONIEC", oznacza to zakończenie wykonywania wszystkich kroków 🏁.
KOD ŹRÓDŁOWY
Ostatnia postać jako "definitywna" (czyli najbardziej konkretna na jaką możemy natrafić), to jest kod źródłowy w jakimś języku programowania 😊. To także jest forma zapisu, gdyż algorytm funkcjonuje w charakterze programu ✅. Oto ten sam program w formie kodu źródłowego w języku Java (taki został ogłoszony we wprowadzeniu do serii) 👇:
public class Main {
public static void main(String[] args) {
for (var i = 1; i <= 100; ++i) {
System.out.println(i);
}
}
}Wypisywanie licznika od 1 do 100, zapewni nam pętla "for" ✅. I to wszystko 😄!
Tyle informacji wystarczy ✔️. Powinieneś/powinnaś już wiedzieć co to jest algorytm, do czego on służy, a także jakie są 3 metody jego przedstawienia 👍. Gdyby coś uciekło z głowy, nie wahaj się tu zajrzeć ponownie 😀!