Dziś wyjaśnimy sobie kolejny znany problem algorytmiczny 😮. Jest to bardzo popularny i ciekawy problem, który posiada pięknie brzmiącą nazwę "problem komiwojażera" 🥾. Rozpatrzymy dzisiaj 2 wersje algorytmów: rozwiązujący ten problem w sposób dokładny i aproksymacyjny ✅. Brzmi nieźle 🙂? No to wchodzić 😄!
PROBLEM KOMIWOJAŻERA NIE JEST TAKI ŁATWY DO ROZWIĄZANIA!
OK, postraszyłem nagłówkiem, jednak najpierw wprowadzę w temat 👻. Problem wędrującego komiwojażera (ang. travelling salesman problem) to popularne zagadnienie polegające na wyznaczeniu optymalnej (czyt. najkrótszej) drogi, która uwzględnia wszystkie kluczowe miejsca do odwiedzenia. Nazwa pochodzi od zajęcia komiwojażera jakim jest właśnie jeżdżenie od domu do domu i oferowanie ludziom składanie zamówień na towary jakie sprzedają (ta część akurat nie wchodzi w problem algorytmiczny 😅) 💵.
PRZEDSTAWIENIE PROBLEMU
Wyobraź sobie, że mamy tytułowego komiwojażera, który musi odwiedzić kilka miast/miejscowości/[tu wstaw własny odpowiednik] 😊. Problem komiwojażera polega na postawieniu kluczowego pytania: "W jakiej kolejności odwiedzić wszystkie miejsca, tak aby dystans całej wędrówki był jak najkrótszy?".
Problem: wyznaczenie najkrótszej drogi do odwiedzenia wszystkich wskazanych lokalizacji
Z algorytmicznego punktu widzenia, to wbrew pozorom stanowi twardy orzech do zgryzienia, tylko nie od strony metodyki, a...obliczeń 😮! Nie chodzi o brak metody - chodzi o jej nieefektywność 💥!
NIE DA SIĘ INACZEJ
Ustalmy fakty. Mamy N miejsc do zbadania. Uznajmy również, że nie wybieramy żadnej pozycji startowej, czyli jesteśmy zmuszeni do sprawdzenia każdej, ale to dosłownie, każdej kombinacji. To co, wystarczy policzyć wszystkie i już 😅? No nie jest tak kolorowo 😏!
 |
Aby rozwiązać problem wędrującego komiwojażera w sposób dokładny, trzeba sprawdzić WSZYSTKIE możliwe kombinacje!!! Podejście takie nazywa się "brute-force".
Źródło: Wikipedia
Metoda pozwalająca na wyznaczenie dokładnego rozwiązania na problem komiwojażera, to "brute-force" i chodzi w niej o zbadanie każdej dozwolonej kombinacji, aby na końcu zwrócić optymalne rozwiązanie ✅. Dokładność rozwiązania, gwarantowana 👍. Prędkość wykonywania, fatalna 👎!
Dysponując przykładowo jedynie 5 lokacjami do zbadania (bez wybierania pozycji startowej), program musi zbadać aż 120 kombinacji i spośród nich wybrać trasę najkrótszą 😱!!! Skąd wiemy, że właśnie tyle?
Selekcja poszczególnych miast jeden po drugim, do złudzenia przypomina permutację bez powtórzeń (kombinatoryka 🙂). Jest to ciąg utworzony ze wszystkich elementów danego zbioru (w tym wypadku, to są lokacje do zbadania). Stąd też, mając do wyboru 5 miast 👇:
C = {a, b, c, d, e}
to jedną ze 120 kombinacji będzie taki ciąg:
{a, b, c, d, e}
natomiast będzie do zbadania również ten:
{a, c, b, d, e}
i ten:
{a, b, c, e, d}
i tak dalej 😰. Nie wysilaj się z policzeniem wszystkich dostępnych kombinacji:
Pn = n!
Wynika stąd, że:
P5 = 5! = 120
Stąd też złożoność czasowa tego problemu wynosi:
O(n!)
i charakteryzuje się wykładniczym wzrostem w czasie 📉!!! Z tego powodu, problem komiwojażera to tzw. "problem NP-zupełny", o którym piszę dużo więcej w osobnym artykule.
Wniosek jest jednoznaczny - "brute-force" nie nadaje się do wyznaczania rozwiązania dla dużych zbiorów danych (dużej liczby lokacji do zbadania).
Wracamy do punktu wyjścia 😧!
Problem: wyznaczenie najkrótszej drogi do odwiedzenia wszystkich wskazanych lokalizacji przy jednoczesnym uniknięciu badania wszystkich dostępnych kombinacji
CZY JESTEŚMY SKAZANI NA PORAŻKĘ?
Skąd 😉. Po prostu trzeba przejść na inną metodę o nieco mniejszej dokładności, lecz o dużo niższej złożoności czasowej ⌚.
Posłużymy się podejściem aproksymacyjnym, czyli metodyki zdolnej do znalezienia rozwiązania zbliżonego do dokładnego. Ważne, aby wiedzieć, że coś zawsze jest za coś ⚠️! Ono może być zadowalające, natomiast nie mamy pewności, że takie będzie zawsze! Rozwiązanie jakie otrzymamy, może być nawet "wyjęte z czapki" 🤭.
Problem komiwojażera można spróbować rozwiązać jeszcze inaczej 🔥. Weźmy jeszcze raz pod lupę te 5 miast 🔍. Możemy na początek wybrać losowo jeden z punktów i sprawdzać resztę z nich po kolei która odległość od tego wybranego do czterech pozostałych będzie jak najmniejsza ✔️. Później konsekwentnie wykreślać pozycje z listy, aż będzie pusta i w taki oto sposób otrzymujemy wynik ostateczny, który kończy się jedynie na kilku iteracjach, zamiast 120 👇:
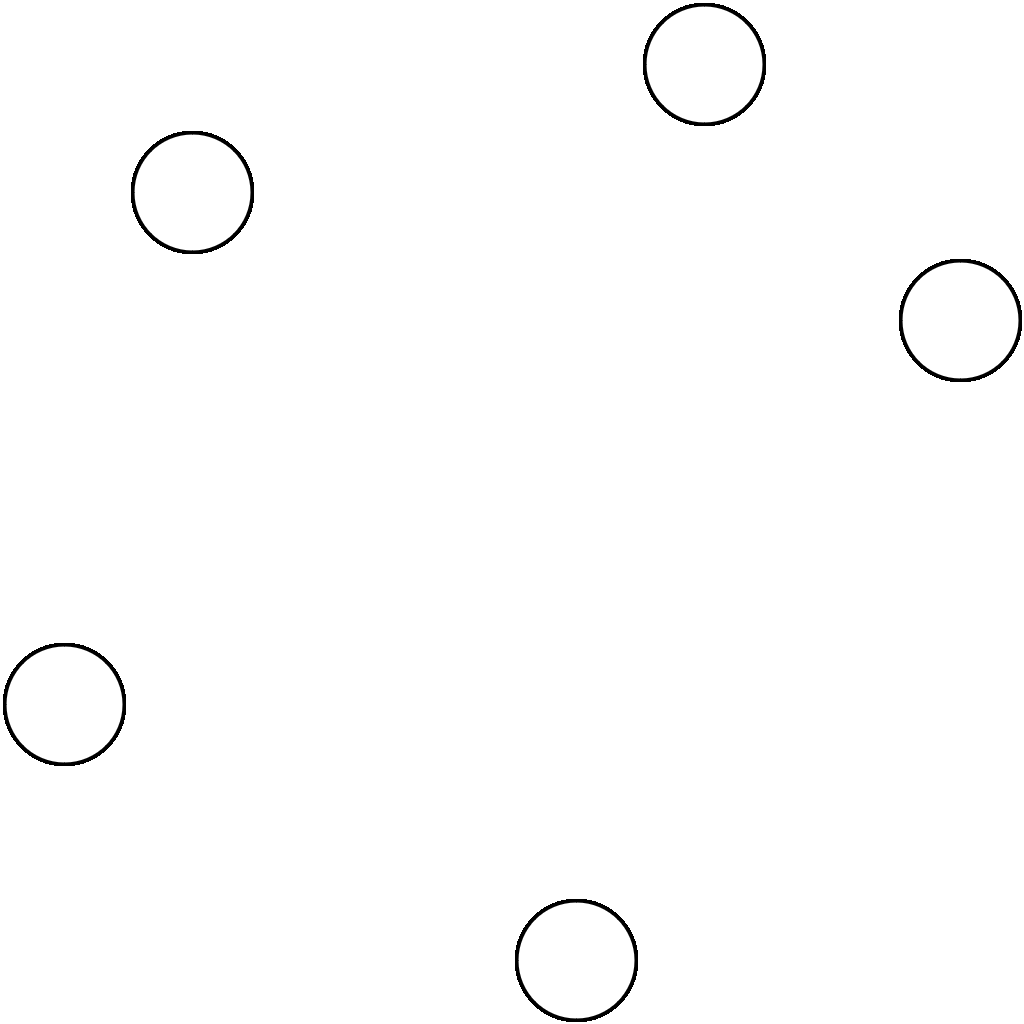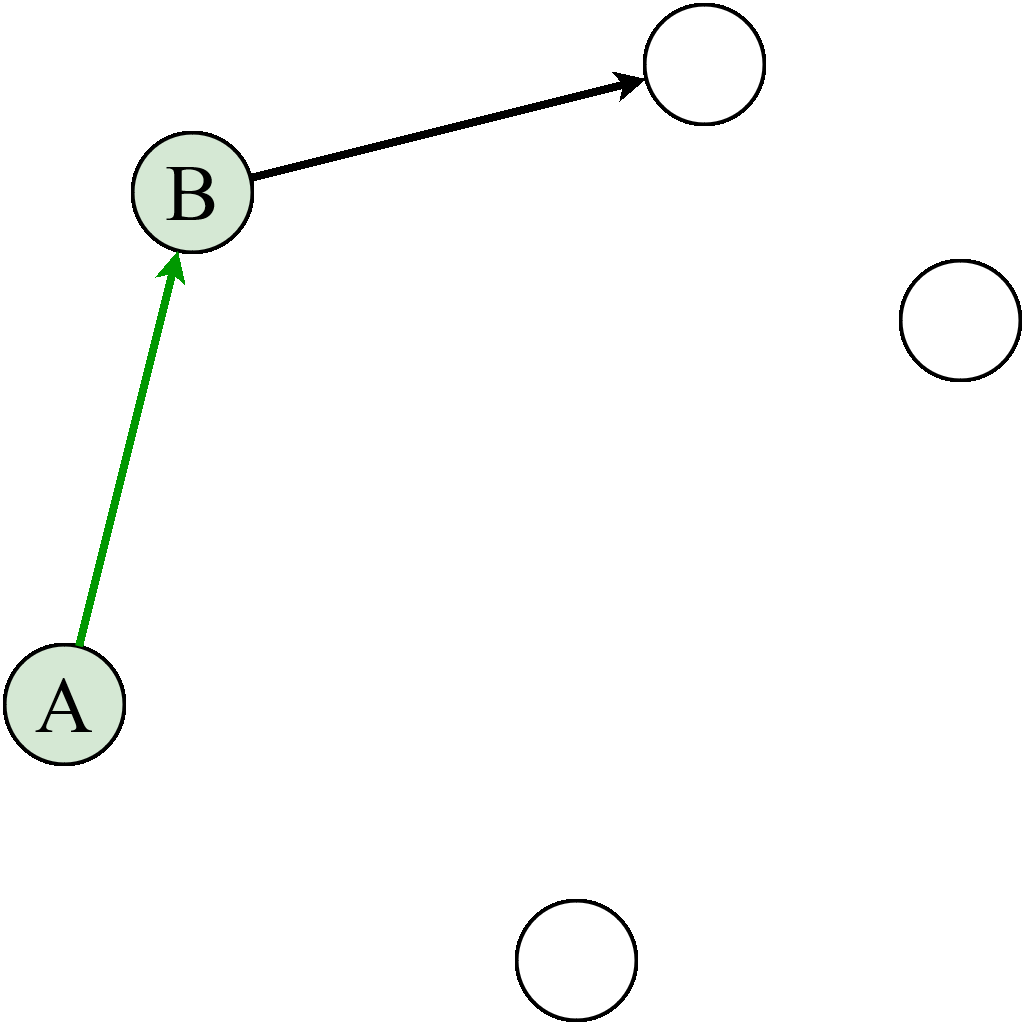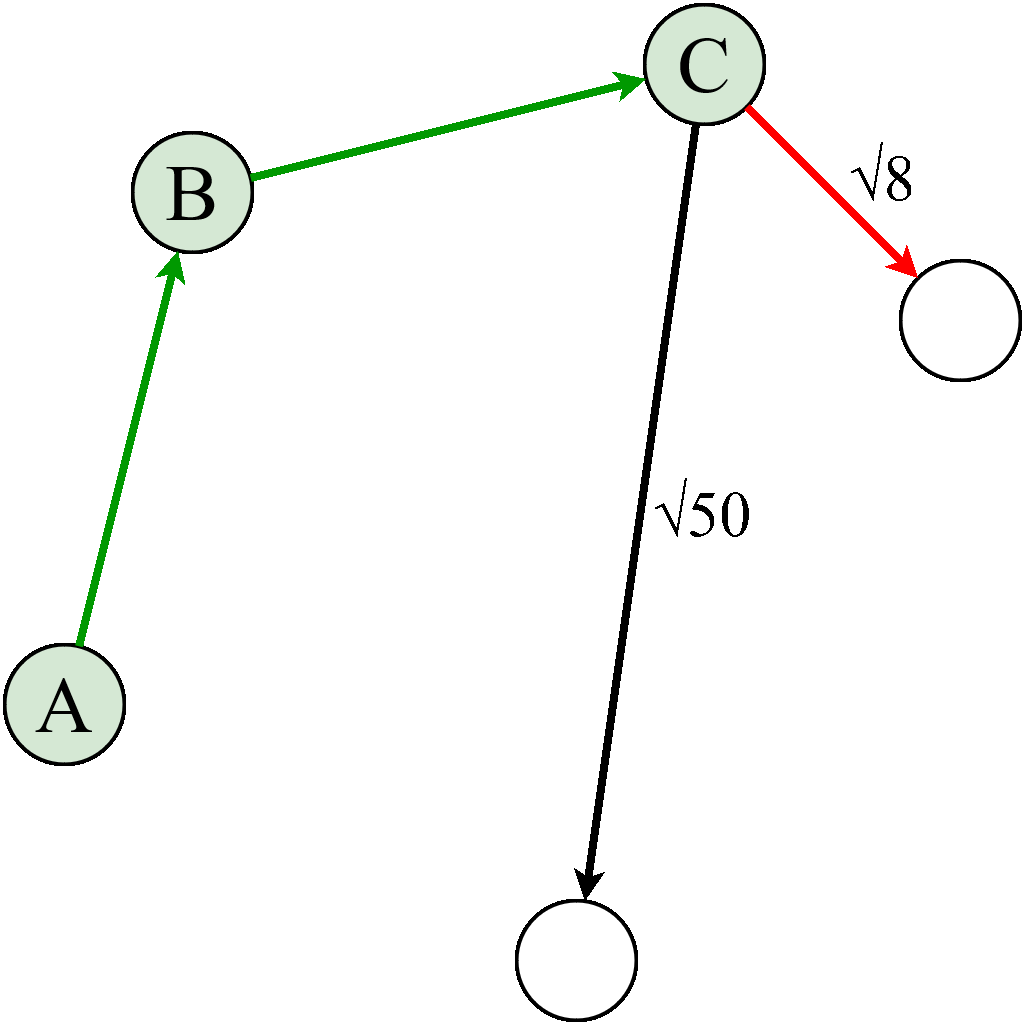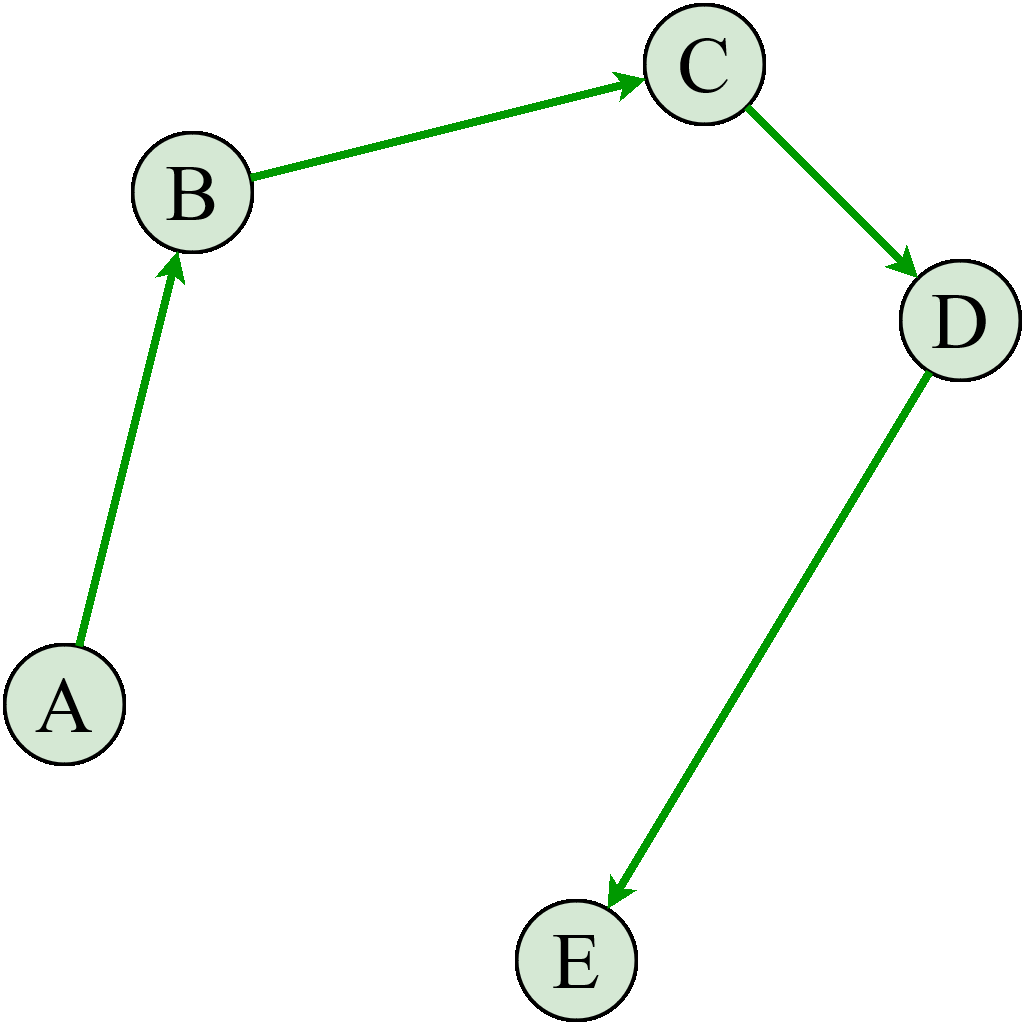 |
Podejście algorytmu aproksymacyjnego rozwiązującego problem komiwojażera.
Pamiętaj - to podejście opiera się na aproksymacji, co oznacza, że nie ma pewności, że wynik będzie zadowalający ‼️. Tutaj, jakość rozwiązania jest obarczona pewnym błędem. On może być mniejszy lub większy, aczkolwiek w większości przypadków on występuje. Natomiast w ramach rekompensaty, zyskujemy na znacznym zredukowaniu złożoności obliczeniowej. To podejście, ma taką złożoność czasową:
O(n2)
zatem, to będzie nas kosztowało "jedynie" n2 podejść 🎯.
Kwadrat dlatego, gdyż dla każdego miejsca, w którym się aktualnie znajdujemy, musimy porównać odległość z każdym innym miejscem. Ta lista stopniowo robi się coraz mniejsza (więc to nie będzie n*n za każdym razem), jednak w notacji dużego O stałe nie grają roli, zatem mamy N do kwadratu 🔵.
KOD ŹRÓDŁOWY
Podsumujmy całą teorię kodem źródłowym w języku Java, z algorytmem rozwiązującym problem komiwojażera stosując podejście aproksymacyjne 💪. Proszę:
KLASA "MAIN"
public class Main {
public static void main(String[] args) {
new Launcher();
}
}Klasa uruchomieniowa jako punkt startowy naszego programu ▶️. Nie trzeba niczego tłumaczyć 😊.
REKORD "POINT"
public record Point(int x, int y) {
public int getDistanceTo(Point point) {
var differenceX = this.x - point.x;
var differenceY = this.y - point.y;
var squaredX = differenceX*differenceX;
var squaredY = differenceY*differenceY;
var distance = Math.sqrt(squaredX + squaredY);
return (int)Math.round(distance);
}
}To jest rekord, w którym zdefiniowano metodę kalkulującą odległość pomiędzy punktami w metryce euklidesowej. Rekord w języku Java jest "skrótem" klasy dysponującej niemodyfikowalnymi danymi składowymi (ze słowem kluczowym "final") wraz z ich akcesorami, czyli metody typu "get" ℹ️.
Słowo "var" oznacza uniknięcie wstawiania typu danych jawnie w kodzie, co jest przyjemnym udogodnieniem ✅. Jeżeli czegokolwiek nie rozumiesz ze składni Javy, to przejdź do załączonych artykułów 😉.
REKORD "CITY"
public record City(String name, Point position) {
public int getDistanceTo(City city) {
return position.getDistanceTo(city.position);
}
}Kolejny osobny rekord do definiowania miast 🏙. Za parametry, przyjmuje nazwę (łańcuch znaków) i punkt w układzie współrzędnych. Dodatkowo, jedna metoda do pobierania odległości między nimi i tyle 😄.
KLASA "TRACK"
import java. util.LinkedHashSet;
public class Track extends LinkedHashSet<City> {
public int getTotalDistanceStartingFrom(City city) {
return stream().filter(cityInTrack -> !cityInTrack.equals(city)).mapToInt(cityInTrack -> cityInTrack.getDistanceTo(city)).sum();
}
}Kolejny składnik naszego programu, tym razem w formie klasy: trasa komiwojażera 🙂. Korzystam z dziedziczenia po kolekcji "LinkedHashSet" ⭐. "HashSet" to jest zbiór, który pilnuje, aby nie wstawiać tych samych (zduplikowanych) elementów do niego (czyli przypadek miasta, które nosi tę samą nazwę i znajduje się w tym samym miejscu 😝). "Linked" oznacza zdolność do zapamiętywania kolejności dodawanych elementów, co w naszym przypadku jest kluczowe, aby otrzymać efekt "dopisywania" kolejnych miast do trasy 👍.
Metoda jaka się tam znajduje, korzysta z podejścia funkcyjnego ⚡. Idąc po kolei 👇:
- "stream" konwertuje kolekcję na strumień - strukturę pozwalającą na manipulacje z użyciem danych,
- "filter" wyklucza dane elementy kolekcji na podstawie zadanego kryterium (predykat),
- "mapToInt" przypisuje każdemu elementowi liczbę otrzymaną na podstawie wyrażenia (w miejscu wyrażenia lambda),
- "sum" sumuje wszystkie uzyskane wartości w kroku poprzednim.
Jednym zdaniem to:
return stream().filter(cityInTrack -> !cityInTrack.equals(city)).mapToInt(cityInTrack -> cityInTrack.getDistanceTo(city)).sum();oznacza: "wyklucz miasto, które jest takie same, jak podane w parametrze, wyznacz odległości między nimi i zsumuj je wszystkie do siebie".
KLASA "CITIES"
import java. util.Optional;
import java. util.Comparator;
import java. util.LinkedHashSet;
public class Cities extends LinkedHashSet<City> {
public Cities() {
add(new City("Warszawa", new Point(-40, 320)));
add(new City("Kielce", new Point(3280, 6709)));
add(new City("Kraków", new Point(456, 746)));
add(new City("Szczecin", new Point(7000, -658)));
add(new City("Wrocław", new Point(15000, -8900)));
}
public Optional<City> getClosestCityTo(City otherCity) {
return stream().min(Comparator.comparingInt(city -> city.getDistanceTo(otherCity)));
}
}To jest drugi zbiór dziedziczący od tego samego "LinkedHashSet", lecz tym razem to są definicje naszych miast, które musi odwiedzić nasz bohater 😊.
W konstruktorze mamy dodawanie instancji, a niżej jest metoda, która także wykorzystuje dobrodziejstwo programowania funkcyjnego. Tutaj:
return stream().min(Comparator.comparingInt(city -> city.getDistanceTo(otherCity)));mamy wyznaczenie odległości pomiędzy każdym miastem, a tym podanym w parametrze ("comparingInt") i zwrócenie na wyjściu tego, do którego dystans jest najkrótszy ("min").
Zwrócę jeszcze uwagę na typ zwracanej wartości ⚠️. Tu mamy niejaki "Optional" - typ "opakowujący" zdefiniowany typ danych, który funkcjonuje jako "osłona" przed wartością "null". Więcej informacji o nim, znajdziesz w załączonym artykule ℹ️.
KLASA "RESULTSPRINTER"
import java. io.PrintStream;
import java. util.function.Function;
public class ResultsPrinter {
private final PrintStream printStream = System.out;
public void printAboutCity(City city, Function<City, String> function, String message) {
printLine(message + function.apply(city));
}
public void printAboutCitiesInTrack(Track track, Function<City, String> function, String message) {
printLine(message);
track.forEach(city -> printLine(function.apply(city)));
}
public void printAboutTrack(Track track, Function<Track, String> function, String message) {
printLine(message + function.apply(track));
}
private void printLine(String message) {
printStream.println(message);
}
}Ostatnia klasa przed algorytmem 😄. To służy tylko do wypisywania komunikatów związanych z przebiegiem działania ⏩. Wydzieloną w ten sposób część kodu możesz łatwo zdemontować, gdy nie będzie Ci już potrzebna 😊.
Może Cię zaciekawić parametr typu "Function", który jest osadzony w metodach 😮. To jest jeden z interfejsów funkcyjnych, a ten rodzaj akurat, pozwala na zwrócenie dowolnego wyrażenia związanego z pierwszym typem parametru w nawiasach kątowych (typ generyczny). Więcej informacji o obu terminach, w załączonych artykułach ✅.
KLASA "LAUNCHER"
import java. util.Random;
public class Launcher {
private final Track track = new Track();
private final Cities leftCities = new Cities();
private final ResultsPrinter resultsPrinter = new ResultsPrinter();
private City currentCity;
public Launcher() {
var startCity = getRandomStartCity();
resultsPrinter.printAboutCity(startCity, City::name, "Wybrane miasto startowe: ");
addCityToTrack(startCity);
determineTrack();
resultsPrinter.printAboutCitiesInTrack(track, City::name, "TRASA: ");
resultsPrinter.printAboutTrack(track, track -> String.valueOf(track.getTotalDistanceStartingFrom(startCity)), "Dystans: ");
}
private City getRandomStartCity() {
var random = new Random();
var citiesArray = leftCities.toArray(new City[0]);
var randomIndex = random.nextInt(0, leftCities.size());
return citiesArray[randomIndex];
}
private void determineTrack() {
while (!leftCities.isEmpty()) {
addClosestCityToTrackIfPossible(currentCity);
}
}
private void addClosestCityToTrackIfPossible(City city) {
var optionalClosestCity = leftCities.getClosestCityTo(city);
optionalClosestCity.ifPresent(this::onNextClosestCityWasFound);
}
private void onNextClosestCityWasFound(City closestCity) {
resultsPrinter.printAboutCity(closestCity, City::name, "Najbliższe miasto to ");
resultsPrinter.printAboutCity(closestCity, city -> String.valueOf(city.getDistanceTo(closestCity)), "Odległość wynosi ");
addCityToTrack(closestCity);
}
private void addCityToTrack(City city) {
track.add(city);
leftCities.remove(city);
currentCity = city;
}
}Dotarliśmy do sedna, czyli do algorytmu rozwiązującego problem komiwojażera w sposób aproksymacyjny 🔔. Przypominam, że korzystamy z aproksymacji dlatego, aby uniknąć nieakceptowalnej złożoności czasowej mogącej przynieść rozwiązanie nawet po kilkuset latach 😅!
U góry deklarujemy sobie 3 dane składowe (i od razu inicjujemy) dla, kolejno 👇:
- trasy dla komiwojażera ("Track"),
- zbioru miast pozostałych do przeanalizowania ("Cities"),
- wypisywania komunikatów podczas działania algorytmu ("ResultsPrinter").
Dodatkowa zmienna prywatna posłuży nam do aktualizowania bieżącego miasta, na którym "stoi" komiwojażer 👍. To jest potrzebne do późniejszego iterowania po pozostałych miejscach 🔁.
Zacznijmy od konstruktora 🔨. Najpierw wyznaczamy sobie losowe miasto, od którego rozpoczniemy wyznaczanie aproksymacyjnie optymalnej trasy uwzględniającej wszystkie miejsca ✔️. Mamy do tego celu metodę, która wyznacza losową liczbę jako indeks tablicy i zwraca taki element 💎.
Ponieważ mamy zbiór miast, a nie listę, nie możemy odwoływać się do elementów przez indeks ⛔. Musimy wpierw skonwertować zbiór na tablicę:
var citiesArray = leftCities.toArray(new City[0]);i wtedy dostać się do elementu stosując notację indeksową 💡.
W kolejnym kroku, dodajemy nasze "startowe miasto" automatycznie do trasy, jako że to będzie nasz pierwszy punkt (bo trasy zawsze zaczynamy od miejsca, od którego zaczynamy 😁). Następnie dochodzimy do "serca" algorytmu - dobieramy kolejne lokalizacje na podstawie odległości w przestrzeni kartezjańskiej ❤️.
Do wykreślania miejsc, mamy pętlę "while" sprawdzającą czy wszystkie dostępne miasta zostały już wyczerpane 0️⃣. Jeżeli jest przynajmniej jedna, to wywołuje się kolejna osobna metoda, której zadaniem jest znalezienie i zwrócenie najbliższego miasta od aktualnego miejsca 🔍. To jest ta metoda, która zwraca typ "Optional" 🎯. Z tego powodu, również od strony pobierania wartości trzeba było zadbać o modyfikację 🔧.
W "Optional" jest tak, że jeżeli ma chronić przed wartościami "null", to należy "opakować" w podobny sposób instrukcje do wykonania. Robimy to w tym miejscu:
optionalClosestCity.ifPresent(this::onNextClosestCityWasFound);"ifPresent" bada czy jest jakaś referencja 👀. Jeżeli jest, to wykonuje się wyrażenie lambda zdefiniowane jako "Consumer" (metoda typu "void" oczekująca jednego parametru typu zgodnego z referencją ℹ️).
Z kolei ten fragment:
this::onNextClosestCityWasFoundto jest nic innego, jak wskazanie tej metody, która ma się wykonać w momencie stwierdzenia, że referencja się znajduje 👍. W tym przypadku zgadza się układ parametrów z "Consumer" z definicją, zatem możemy skorzystać z referencji do metody 💪!
Sama metoda wywołuje inne metody do wypisania szczegółów na temat kolejnego wyznaczonego miasta do trasy, a na końcu wywołuję już ostatnią metodę w tej klasie 🙂. Ona dodaje miasto do trasy, jednocześnie usuwa je z listy dostępnych miast i przypisuje referencję do "obecnego miasta" ✅.
Powtarzamy tę operację, aż do wyczerpania listy miast pozostałych do zbadania 💯. Potem algorytm kończy swoje działanie 🏁.
A ja w tym miejscu kończę omawiać problem komiwojażera 😊. Zagadnienie same w sobie jest ciekawe, gdyż wymaga bardziej sprytnego podejścia niż "brute-force" i "latanie" po wszystkich kombinacjach jak leci 😄. To, co zaprezentowałem, stanowi jedno z co najmniej kilkunastu podejść aproksymacyjnych, czyli alternatywnych podejść rozwiązujących ten problem 🔥. Przeanalizuj sobie całość i poeksperymentuj z różnymi kombinacjami danych 😉!