W kolejnym artykule o algorytmice, czas poruszyć jeden, bardzo znany i ważny algorytm umożliwiający wyznaczanie ścieżki do wskazanego węzła w grafie ważonym 🤩! Temat niniejszego artykułu to algorytm Dijkstry, także usiądź sobie wygodnie i czytaj z dużą uwagą 🫵!
ALGORYTM DIJKSTRY. ALGORYTM, O KTÓRYM USŁYSZYSZ NIEJEDEN RAZ!
Algorytm dobrze znany z nazwy, którą jest szansa, że mogłeś(-aś) już usłyszeć 👂. Powstały z inicjatywy bardzo ważnej postaci w nauce informatycznej, Edsgera Dijkstry - informatyka holenderskiego pochodzenia, który spopularyzował programowanie strukturalne w słynnej pracy "Go To Statement Considered Harmful" (1968) 🔥.
Sprawdźmy co to takiego, że jest powszechnie znane i cenione 🔍.
ALGORYTM DIJKSTRY JAKO "PIĘTRO WYŻEJ" W WYZNACZANIU ŚCIEŻKI W GRAFIE
Ten algorytm także rozwiązuje problem wyszukiwania najkrótszej ścieżki (ang. shortest path problem), z tym że w tym przypadku jest możliwe rozróżnienie wag krawędzi (w odróżnieniu od przeszukiwania wszerz) 🤩! Tutaj zróbmy przystanek na szybkie wyjaśnienie grafu ważonego i znaczenia pojęcia "waga krawędzi" 💪.
GRAF WAŻONY
Królowa nauk dysponuje wieloma rodzajami grafu. Jednym z nich, jest graf ważony. Charakteryzuje się tym, że każdej krawędzi (tzn. połączeniu pomiędzy jednym węzłem, a drugim), przypisywana jest pewna liczba 🔢. Wartość liczbowa znowu zależy od kontekstu i postawionego problemu. W przypadku wyznaczania ścieżki, oznacza koszt lub "wysiłek" jaki trzeba ponieść, aby przedostać się od jednego węzła do drugiego 💸.
Dla lepszego zobrazowania sytuacji, wyobraź sobie chęć przedostania się na drugą stronę rzeki 🌉. Masz 2 opcje do wyboru 👇:
- przepłynąć przez rzekę na drugą stronę (wpław),
- pójść kawałek dalej drogą i przejść przez most.
Przepłynięcie będzie o wiele bardziej wymagające, niż skorzystanie z mostu 😰. Wtedy, dzięki różnym wagom, możesz nadać model grafowi (który w tym przypadku reprezentuje mapę) i nadać różne wagi różnym węzłom zgodnie z własną topologią 👍. Węzły oznaczające w danym miejscu rzekę, będą "ważyły" np. 10x tyle, a droga razem z mostem będzie "kosztować standardowo" (bez zmian) ℹ️.
W taki właśnie sposób możesz definiować różne przeszkody czy niekorzystny teren do przebrnięcia i algorytm Dijkstry doskonale sobie poradzi z rozróżnieniem 🏆. "Pathfinding" to jego specjalność 😄!
GRAF SKIEROWANY
Od razu przedstawię Ci kolejny rodzaj grafu, który też ma związek z algorytmem Dijkstry - graf skierowany ▶️. Graf skierowany to taki graf, którego relacje są skierowane tj. określają kierunek od którego węzła do którego, możemy się poruszać. Co ważne, to przejście jest "jednokierunkowe" ➡️.
Przykładowo, jeżeli masz 2 węzły (A i B) i zachodzi między nimi relacja, to "zwrot" tej relacji w kierunku węzła B oznaczać będzie: "możesz od węzła A, przejść do węzła B" 🔓. Natomiast, nie jest możliwe przedostanie się na odwrót 🚫!
Teraz możemy iść dalej 😅!
OGRANICZENIE, KTÓREGO MUSISZ BYĆ ŚWIADOMY(-A)
Muszę nieco przyblokować Twój "hurra optymizm", jeśli taki pojawił się w głowie ✋. Algorytm Dijkstry, choć potrafi wyznaczyć ścieżkę od jednego miejsca do drugiego, to jednak nie przyniesie dobrych rezultatów jeśli nie spełnia pewnych wymagań.
Warunkiem zwrócenia prawidłowego rozwiązania jest to, że wszystkie wagi (krawędzie) danego grafu muszą być nieujemne. Jeżeli program gdziekolwiek trafi na krawędź o ujemnej wadze, to się "wykopyrtnie" i rozwiązanie nie będzie optymalne (w dalszej części tłumaczę dlaczego ℹ️) ❌!
Jeżeli bardzo będzie Ci zależało na zachowaniu wag ujemnych, to czeka Cię przesiadka na algorytm Bellmana-Forda - to jest odmiana algorytmu Dijkstry zapewniająca wyznaczenie prawidłowego rozwiązania na grafach z krawędziami o wartościach ujemnych 💡.
Po tak wyłożonej teorii, zapraszam do dalszej części ukazującej jak algorytm Dijkstry wyznacza rozwiązanie krok po kroku 🔍.
DZIAŁANIE ALGORYTMU DIJKSTRY
Wszystko zaczyna się od danych wejściowych 🙂. Mamy taki graf 👇:
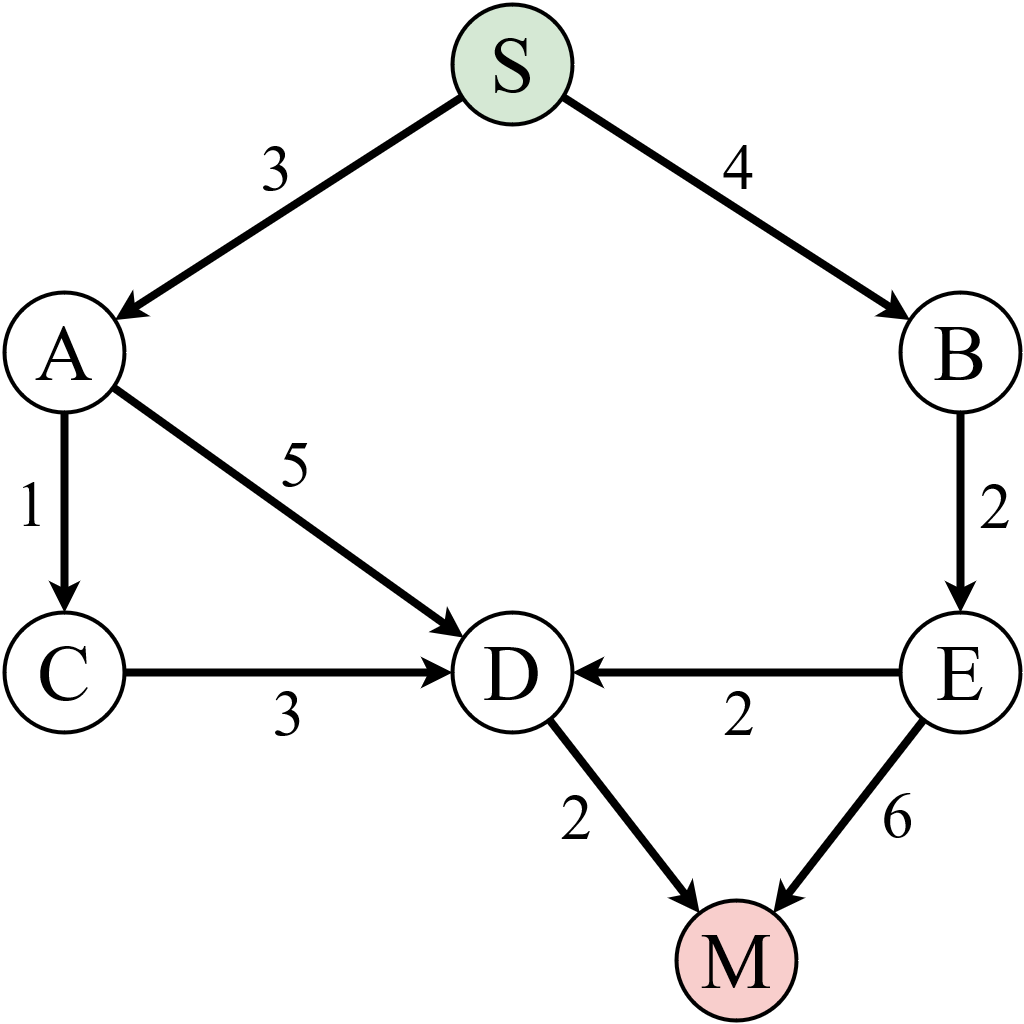 |
Rysunek graficzny prezentujący graf ważony.
i chcemy przedostać się przez węzły od węzła startowego (litera 'S', kolor zielony) do węzła docelowego (litera 'M', kolor czerwony).
Problem: wyznaczenie ścieżki do wskazanego węzła w grafie ważonym na podstawie podanego kryterium
Można wyjaśniać 😎!
Algorytm Dijkstry wykorzystuje dwie tabelki 2️⃣:
- tabela kosztów - określa określa koszty dotarcia do danego węzła,
- tabela rodziców - reprezentuje "rodziców" wszystkich węzłów z wyjątkiem węzła startowego (to przyda się do wyznaczania ścieżki od węzła początkowego, do docelowego).
Przyjrzyjmy się tym tabelom 👀.
TABELA KOSZTÓW
Tabela kosztów przedstawia wagi krawędzi jako określenie wydatku czasu ⌚, energii ⚡ bądź pieniędzy 💵 ile trzeba przeznaczyć na dotarcie do danego węzła ✅.
My na samym początku, znamy koszty dotarcia jedynie do tych węzłów, które są w bezpośredniej relacji z naszym punktem startowym. Przy całej reszcie nie wiadomo na chwilę obecną ile kosztów trzeba ponieść, zatem umownie określamy je znakiem nieskończoności 🔁.
Na wstępie, tabelka kosztów dotarcia do poszczególnych węzłów będzie wyglądała tak 👇:
| NAZWA WĘZŁA | KOSZT DOTARCIA DO WĘZŁA (WAGA KRAWĘDZI) |
| A | 3 |
| B | 4 |
| C | ∞ |
| D | ∞ |
| E | ∞ |
| M | ∞ |
TABELA RODZICÓW
Tabela rodziców przechowuje informacje na temat relacji pomiędzy węzłami, czyli które z relacji wskazują na które węzły 🫵. Dzięki niej, będziemy mogli wyznaczyć ścieżkę od końca do początku (bo tak działa wyznaczanie ścieżki) 🤩! Przez "rodzica" należy rozumieć węzeł, od którego można dojść do węzła sąsiedniego.
Postępujemy bardzo podobnie co wyżej, z tym że po prawej stronie zamiast wartości liczbowych, wskazujemy na nazwę węzła będącego bezpośrednim sąsiadem, a wszelkie nieznane nam informacje, oznaczamy znakiem zapytania:
| NAZWA WĘZŁA | NAZWA WĘZŁA "RODZICA" |
| A | Start |
| B | Start |
| C | ? |
| D | ? |
| E | ? |
| M | ? |
Po opracowaniu tych tabelek, algorytm Dijkstry rozpoczyna swoje działania 🚀! Spróbuj już teraz odgadnąć jaka struktura danych będzie pasowała jak ulał do przechowania tych informacji 😉.
PROCES BADANIA WĘZŁÓW
Uwaga! W tej części będę używał kolorów, aby ułatwić zrozumienie tematu, bo to zagadnienie nie będzie od samego początku dla Ciebie jasne 😅!
Patrząc na rysunek grafu powyżej, widzimy że punkt startowy łączą 2 węzły: węzeł A i węzeł B ℹ️. Algorytm każdorazowo wybiera ten węzeł, który spełnia 2 warunki 👇:
- węzeł nie został jeszcze zbadany (oznaczony jako "odwiedzony"),
- koszt dotarcia do węzła jest najmniejszy.
Także najpierw weźmie pod uwagę węzeł A i zbada koszty wszystkich jego sąsiadów 🔍. Dla każdego węzła sąsiedniego, algorytm Dijkstry oblicza sumę kosztu dotarcia do węzła A i kosztu jego sąsiada 💥.
Jeżeli okaże się, że ta suma jest mniejsza od kosztu dotarcia do sąsiada odnotowanego w tabelce, to aktualizuje wpis w tabeli kosztów i rodziców 🎉:
- do tabeli kosztów przypisuje tańszy koszt dotarcia do węzła sąsiedniego,
- do tabeli rodziców przypisuje sąsiadowi rodzica (węzeł A).
Algorytm wykonuje to samo dla każdego sąsiedniego węzła, aż do "wyczerpania zapasów" 🙂.
Kiedy wszystkie węzły sąsiednie zostaną przeanalizowane, to węzeł A (węzeł, który został wybrany na samym początku) zostaje oznaczony jako "odwiedzony" ✅, a algorytm wybiera kolejny węzeł o najmniejszym koszcie ▶️. Jeżeli wszystkie węzły już zostały zbadane, działanie zostaje zakończone. Na sam koniec algorytm "zagląda" do tabeli rodziców i na jej podstawie wyznacza ścieżkę od węzła początkowego do docelowego ✏️. Te informacje wystarczą w zupełności, aby "narysować" drogę 🧨.
Tak w dużym skrócie funkcjonuje algorytm Dijkstry 🎯!
ILE TO WSZYSTKO "KOSZTUJE" OBLICZENIOWO?
Podsumujmy. Mamy graf, węzły i krawędzie. Przy każdej iteracji ustalamy węzeł o najniższym dotychczasowym koszcie raz po raz ❌. Później dla każdego węzła, badamy wszystkich jego sąsiadów, czyli mamy drugie tyle 😲.
Biorąc wszystko do kupy, otrzymujemy taką złożoność obliczeniową w notacji dużego O 👇:
O(|V|2) : V = zbiór wierzchołków
Kwadrat z mocy zbioru wierzchołków (węzłów), czyli kwadrat liczby węzłów w grafie 💥. Tyle wyjdzie w praktyce za każdym razem, ponieważ algorytm Dijkstry musi przeanalizować cały graf celem zapewnienia optymalnej ścieżki, bez względu na to, jak szybko docelowy węzeł zostanie znaleziony (bo zawsze może być jakaś lepsza ścieżka) 🎯!
Warto nadmienić, że to nie jest sztywna złożoność czasowa algorytmu Dijkstry samego w sobie ⚠️! To jest złożoność obliczeniowa implementacji liniowej, jaką demonstruję poniżej 🧠. Implementacja liniowa tym się charakteryzuje, że za każdym razem wyznaczamy węzeł o najniższym koszcie "ręcznie" ✊. To nie jest efektywne podejście, lecz najprostsze do zrozumienia 💡.
Przy użyciu kolejki priorytetowej (struktury danych sortującej automatycznie elementy po wskazanej składowej ℹ️), można zredukować złożoność czasową do nieco lepszej postaci. Więc tak naprawdę odpowiedź na to pytanie brzmi "to zależy jak to zaprogramujesz" 😉.
KOD ŹRÓDŁOWY
Doszliśmy do praktyki i prawdopodobnie najbardziej interesującego podpunktu moich artykułów, jakim jest gotowy kod źródłowy w języku Java 😊! Częstuj się nim 🍰!
KLASA "MAIN"
public class Main {
public static void main(String[] args) {
new Launcher();
}
}Jak zwykle, zaczynamy od samego uruchomienia programu, więc klasa "Main" będzie pierwszą jaka zostanie wykonana, a w niej mamy instancję klasy uruchamiającej nasz kod algorytmiczny 🚀!
KLASA "NODE"
import java. util.LinkedHashMap;
public class Node {
private final String name;
private final LinkedHashMap<Node, Integer> neighbours = new LinkedHashMap<>();
private boolean isVisited;
@Override
public String toString() {
return getName();
}
@Override
public int hashCode() {
return getName().hashCode();
}
@Override
public boolean equals(Object object) {
if(getClass() != object.getClass()) {
return false;
}
var node = (Node)object;
return getName().equals(node.getName());
}
public Node(String name) {
this.name = name;
}
public void addNodeAsNeighbour(Node node, int costToReach) {
neighbours.put(node, costToReach);
}
public void setAsVisited() {
isVisited = true;
}
public String getName() {
return name;
}
public LinkedHashMap<Node, Integer> getNeighbours() {
return neighbours;
}
public boolean isVisited() {
return isVisited;
}
}Ta klasa pozwoli nam tworzyć pojedyncze węzły grafu 🌟. Mamy 3 składowe 👇:
- łańcuch znaków jako nazwa,
- słownik do przechowywania węzłów sąsiednich (korzystam ze słownika, aby móc definiować koszt dotarcia do węzłów sąsiednich "wychodzących" od tego węzła),
- wartość logiczna (flaga) czy węzeł został już odwiedzony.
Wstawiłem słownik, gdyż w przypadku definiowania węzłów sąsiednich ważone są nie same węzły, tylko przejścia między nimi, czyli relacje ⚠️! Słownik jest typu "Linked" co oznacza, że kolejność wprowadzanych rekordów do niego będzie zapamiętywana 🧠. Modyfikator "final" oznacza, że raz przypisanej wartości do danej zmiennej nie można zmienić - nie ma potrzeby zmieniania nazwy węzłom ani alokowania nowych pamięci dla słowników 🔒.
Przesłaniamy niektóre metody pochodzące od klasy "Object", która jest "matką" wszystkich klas w Javie:
- "toString" w celu zdefiniowania łańcucha znaków jaki ma się wyświetlać w komunikatach po podaniu samego obiektu z referencją (bez metod pobocznych),
- "hashCode" w celu zdefiniowania wartości dla kodu skrótu, aby wpływać na ustalanie czy dwa węzły są sobie równe,
- "equals" z tego samego powodu, co w pkt. 2.
Kolejne metody (bez adnotacji "Override") są następujące:
- konstruktor do nadawania nazwy węzłowi,
- "addNodeAsNeighbour" do dodawania wskazanego węzła jako sąsiada danego węzła wraz z przypisanym kosztem odpowiadającym budowie węzła,
- "setAsVisited" do "oznaczania" węzła jako "odwiedzonego",
- "getName" do pobierania nazwy węzła,
- "getNeighbours" do pobierania słownika z węzłami sąsiednimi i kosztami dotarcia do nich od tego węzła,
- "isVisited" do pobierania stanu węzła czy został "odwiedzony".
I na sam koniec informacja, że możesz skorzystać ze słowa kluczowego "var" do ominięcia jawnego wpisywania określonego typu danych 🙂.
KLASA "GRAPH"
import java. util.Arrays;
import java. util.LinkedHashSet;
public class Graph extends LinkedHashSet {
private final Node startNode = new Node("S");
private final Node nodeA = new Node("A");
private final Node nodeB = new Node("B");
private final Node nodeC = new Node("C");
private final Node nodeD = new Node("D");
private final Node nodeE = new Node("E");
private final Node targetNode = new Node("M");
public Graph() {
addAll(Arrays.asList(startNode, nodeA, nodeB, nodeC, nodeD, nodeE, targetNode));
configureNeighbours();
}
public Node getStartNode() {
return startNode;
}
private void configureNeighbours() {
startNode.addNodeAsNeighbour(nodeA, 3);
startNode.addNodeAsNeighbour(nodeB, 4);
nodeA.addNodeAsNeighbour(nodeC, 1);
nodeA.addNodeAsNeighbour(nodeD, 5);
nodeB.addNodeAsNeighbour(nodeE, 2);
nodeC.addNodeAsNeighbour(nodeD, 3);
nodeD.addNodeAsNeighbour(targetNode, 2);
nodeE.addNodeAsNeighbour(nodeD, 2);
nodeE.addNodeAsNeighbour(targetNode, 6);
}
} To jest klasa już dla całego grafu 🧨. Dziedziczymy sobie od "HashSet" (zbiór), bo chcemy zapobiec potencjalnej sytuacji dodawania dwóch takich samych węzłów (z takimi samymi nazwami). "LinkedHashSet", aby kolejność dodawanych elementów była nietknięta 🚫.
Na samej górze, definiujemy sobie obiekty węzłów nadając każdemu z nich nazwę ▶️. W konstruktorze, wywołujemy 2 metody 👇:
- "addAll" do wygodnego dodania wielu węzłów naraz (aby to uczynić, musimy otoczyć całość wewnętrznym wywołaniem "Arrays.asList"),
- nasza własna, do konfiguracji połączeń pomiędzy węzłami.
Niżej konstruktora, mamy kolejne 2 metody 2️⃣. Ta najkrótsza, pobiera referencję do węzła początkowego (to nam się przyda do wykluczania wpisywania tego węzła do tabeli z danymi ❌). Ta na samym dole, tworzy połączenia pomiędzy węzłami 🔌. Robimy to poprzez wywołanie metody z klasy "Node", w której wskazujemy węzeł, do którego ma zostać połączona relacja skierowana i koszt dotarcia do niego, gdybyśmy zaczynali od tego węzła 💸.
KLASA "NODESTABLEROWDATA"
public class NodesTableRowData {
private int cost;
private Node parentNode;
@Override
public String toString() {
return "{Koszt: " + cost + ", węzeł \"rodzic\": " + parentNode + "}";
}
public NodesTableRowData(int cost, Node parentNode) {
setValues(cost, parentNode);
}
public void setValues(int cost, Node parentNode) {
this.cost = cost;
this.parentNode = parentNode;
}
public int getCost() {
return cost;
}
}Tutaj mamy klasę pomocniczą dla pojedynczego wiersza naszej tabeli do rejestrowania dotychczasowych ustaleń dla każdego z węzłów (tak, jak tłumaczyłem wyżej) 📝.
Mamy 2 składowe 👇:
- aktualnie odnotowany koszt (to nie jest koszt rzeczywisty wynikający z grafu, tylko regularnie aktualizowany przez nas, tak jakbyśmy notowali bieżąco na kartce ✍️),
- referencja do węzła "rodzica".
Tutaj też przesłaniamy sobie metodę "toString", aby w komunikatach było widać informacje na temat pojedynczego wiersza tabeli ℹ️. W konstruktorze wywołujemy metodę do zmiany danych w naszym wierszu tj. nowy koszt i nowy węzeł "rodzic" 🔥. A niżej znajduje się metoda pobierająca aktualnie wpisany koszt 🙂.
KLASA "NODESDATATABLE"
import java. util.LinkedHashMap;
public class NodesTable extends LinkedHashMap<Node, NodesTableRowData> {
@Override
public String toString() {
var stringBuilder = new StringBuilder();
forEach((key, value) -> stringBuilder.append(key).append(" -> ").append(value).append("\n"));
return stringBuilder.toString();
}
public void putInitialData(Graph graph, Node startNode) {
var nodesWithoutStartNode = graph.stream().filter(node -> !node.getName().equals(startNode.getName()));
nodesWithoutStartNode.forEach(node -> put(node, getNodeTableRowData(startNode, node)));
}
private NodesTableRowData getNodeTableRowData(Node startNode, Node neighbour) {
var neighboursOfStartNode = startNode.getNeighbours();
var costToReach = neighboursOfStartNode.getOrDefault(neighbour, Integer.MAX_VALUE);
var parentNode = neighboursOfStartNode.containsKey(neighbour) ? startNode : null;
return new NodesTableRowData(costToReach, parentNode);
}
}To jest miejsce dla całej naszej "tabeli" 🧡! Tu też mamy dziedziczenie od "LinkedHashMap", także do danego węzła przypisujemy rekord z danymi (poprzednia klasa) 👍.
U samej góry, przesłaniamy sobie "toString", aby uwidocznić w przyjemny sposób aktualną postać całej naszej tabeli w konsoli ("println") 😊. Ponieważ co wiersz z danymi "doklejamy" nowy łańcuch znaków, użyłem obiektu "StringBuilder", aby zapobiec wyciekom pamięci ⚠️.
Te "forEach", to nie jest pętla rozszerzona, tylko tzw. "funkcja wyższego rzędu" (więcej informacji w załączonym artykule ℹ️).
Jedyna metoda o publicznym dostępie, ma za zadanie umieścić do naszej "tabeli" dane wstępne (to, co wiemy na samym początku) ✒️. Aby wykluczyć węzeł początkowy i nie uwzględniać go w danych, korzystam z podejścia funkcyjnego polegającego na użyciu strumienia ("stream") i filtracji ("filter"). To 👇:
var nodesWithoutStartNode = graph.stream().filter(node -> !node.getName().equals(startNode.getName()));oznacza: "zamień elementy grafu na strumień i wyklucz te węzły, których nazwa pokrywa się z nazwą węzła początkowego" 😅.
Następnie, dla każdego innego węzła ("forEach"), wstawiamy sobie wiersz z danymi do słownika używając metody "put" 💡. Kluczem jest węzeł 🔑, a wartością, nasza instancja reprezentująca wiersz w tabeli 💯. Natomiast nie tworzymy jej bezpośrednio, tylko wywołujemy metodę niżej, aby odpowiednio przygotowała nam ten wiersz.
Metoda tworząca wiersz z danymi potrzebuje informacji na temat węzła początkowego, a konkretniej, jego węzłów sąsiednich ℹ️. Następnie, ustala wstępny koszt i węzła "rodzica" w następujący sposób:
- jeżeli dany węzeł jest sąsiadem węzła początkowego, to:
- koszt do zanotowania = koszt dotarcia do węzła od węzła początkowego,
- węzeł "rodzic" = węzeł początkowy,
- jeżeli dany węzeł nie jest sąsiadem węzła początkowego, to:
- koszt do zanotowania = nieskończoność (tu używam "Integer.MAX_VALUE" jako "umowna nieskończoność", czyli (231 - 1), bo w informatyce wszystko jest skończonym ciągiem bitów),
- węzeł "rodzic" = "null" (nieznany).
Po ustaleniu danych w powyższy sposób, na wyjściu zwracany jest nowy obiekt jako pojedynczy wiersz z danymi 👍.
KLASA "RESULTSPRINTER"
import java. io.PrintStream;
import java. util.function.Function;
public class ResultsPrinter {
private final PrintStream printStream = System.out;
public void printAboutGraph(Graph graph, String message) {
printLine(message);
graph.forEach(this::printAboutNodeInGraph);
}
public void printAboutTable(NodesTable nodesTable, String message) {
printLine(message + nodesTable);
}
public void printAboutNode(Node node, Function<Node, String> function, String message) {
printLine(message + function.apply(node));
}
public void printAboutNodeData(NodesTableRowData nodesTableRowData, String message) {
printLine(message + nodesTableRowData);
}
public void printAboutInteger(int integer, String message) {
printLine(message + integer);
}
private void printAboutNodeInGraph(Node node) {
printLine(node.getName());
node.getNeighbours().forEach((neighbour, neighbourCost) -> printLine("\t" + neighbour.getName()));
}
private void printLine(String message) {
printStream.println(message);
}
}To jest klasa wypisująca nam komunikaty dla różnych typów danych ℹ️. Nie ma sensu tłumaczyć każdej po kolei, skupię się tylko na parametrze typu "Function", który nie jest tak często widziany w przykładowych kodach źródłowych 😲. To jest interfejs funkcyjny pozwalający na wstawienie żywej treści metody w miejsce parametru (w formie wyrażenia lambda) ⭐! Ta postać 👇:
Function<Node, String>oznacza w tym przypadku pobieranie parametru jako węzła i zwrócenie na wyjściu łańcucha znaków 💥. Po więcej informacji, zapraszam do stosownego artykułu 👆.
KLASA "LAUNCHER"
import java. util.Map;
import java. util.Optional;
import java. util.Comparator;
public class Launcher {
private final Graph graph = new Graph();
private final NodesTable nodesTable = new NodesTable();
private final ResultsPrinter resultsPrinter = new ResultsPrinter();
public Launcher() {
resultsPrinter.printAboutGraph(graph, "Węzły w grafie: ");
nodesTable.putInitialData(graph, graph.getStartNode());
printAboutTable();
findPath();
printAboutTable();
}
private void printAboutTable() {
resultsPrinter.printAboutTable(nodesTable, "\nDane węzłów: \n");
}
private void findPath() {
Optional<Node> optionalUnvisitedNodeWithLowestCost;
while ((optionalUnvisitedNodeWithLowestCost = getUnvisitedNodeWithLowestCost()).isPresent()) {
handleNode(optionalUnvisitedNodeWithLowestCost.get());
}
}
private Optional<Node> getUnvisitedNodeWithLowestCost() {
var unvisitedNodesFromGraph = graph.stream().filter(node -> !node.isVisited()).toList();
var unvisitedNodesFromTable = nodesTable.entrySet().stream().filter(entry -> unvisitedNodesFromGraph.contains(entry.getKey()));
var unvisitedNodeTableRowDataWithLowestCost = unvisitedNodesFromTable.min(Comparator.comparing(entry -> entry.getValue().getCost()));
var optionalUnvisitedNodeWithLowestCost = unvisitedNodeTableRowDataWithLowestCost.map(Map.Entry::getKey);
return optionalUnvisitedNodeWithLowestCost.flatMap(unvisitedNodeWithLowestCost -> unvisitedNodesFromGraph.stream().filter(node -> node.getName().equals(unvisitedNodeWithLowestCost.getName())).findFirst());
}
private void handleNode(Node node) {
resultsPrinter.printAboutNode(node, Node::getName, "\nObecny węzeł: ");
handleNeighboursOfNode(node);
node.setAsVisited();
}
private void handleNeighboursOfNode(Node node) {
var nodeNeighbours = node.getNeighbours();
nodeNeighbours.entrySet().forEach(neighbourDataFromGraph -> updateNodesTableRowDataIfNeeded(neighbourDataFromGraph, node));
}
private void updateNodesTableRowDataIfNeeded(Map.Entry<Node, Integer> neighbourFromGraphEntry, Node parentNode) {
var neighbourFromGraph = neighbourFromGraphEntry.getKey();
var costOfNeighbourFromGraph = neighbourFromGraphEntry.getValue();
var parentDataFromTable = nodesTable.get(parentNode);
var neighbourDataFromTable = nodesTable.get(neighbourFromGraph);
var costOfParentFromTable = parentDataFromTable.getCost();
var costOfNeighbourFromTable = neighbourDataFromTable.getCost();
var currentTotalCostOfNeighbour = costOfParentFromTable + costOfNeighbourFromGraph;
resultsPrinter.printAboutNode(neighbourFromGraph, Node::getName, "\nObecny węzeł sąsiedni: ");
resultsPrinter.printAboutInteger(costOfNeighbourFromGraph, "Koszt dotarcia do węzła sąsiedniego w grafie: ");
resultsPrinter.printAboutInteger(costOfParentFromTable, "Obecny koszt węzła \"rodzica\" w tabeli: ");
resultsPrinter.printAboutInteger(costOfNeighbourFromTable, "Obecny koszt węzła sąsiedniego w tabeli: ");
resultsPrinter.printAboutInteger(currentTotalCostOfNeighbour, "Całkowity koszt dotarcia do węzła sąsiedniego w grafie: ");
if(costOfNeighbourFromTable > currentTotalCostOfNeighbour) {
neighbourDataFromTable.setValues(currentTotalCostOfNeighbour, parentNode);
resultsPrinter.printAboutNodeData(neighbourDataFromTable, "Aktualizuję dane w tabeli: ");
}
}
}Jesteśmy przy ostatniej, największej klasie ukazującej algorytm Dijkstry 💣! Kod źródłowy jest dużo większy, niż przy pozostałych przykładach jakie ukazałem, więc staram się wszystko wytłumaczyć ze szczególną starannością ✅.
Najpierw definiujemy sobie 3 składowe (tym razem wszystkie "finalne" 😉) 👇:
- obiekt grafu,
- obiekt tabeli do regularnego aktualizowania danych,
- obiekt do wypisywania komunikatów w konsoli.
Konstruktor, tak jak cała reszta klas, inicjuje nam obiekt 🔧. W tym przypadku, robimy 3 rzeczy:
- wypisujemy sobie komunikaty do prezentacji węzłów sąsiednich węzłów w grafie,
- wstawiamy wstępne dane do tabeli,
- uruchamiamy algorytm Dijkstry 😄.
Czas wytłumaczyć w końcu sam algorytm 💪!
"Sercem" algorytmu Dijkstry jest pętla "while" 🔁. Na samym początku, jak co każdą iterację, pobieramy sobie niezbadany węzeł o odnotowanym najniższym koszcie 1️⃣. Korzystam z nietypowego zagnieżdżenia instrukcji przypisującej w miejsce sprawdzania warunku w pętli:
while ((optionalUnvisitedNodeWithLowestCost = getUnvisitedNodeWithLowestCost()).isPresent()) {
handleNode(optionalUnvisitedNodeWithLowestCost.get());
}Dzięki temu, unikam "rozprowadzenia" tego samego przypisania na zewnątrz pętli i w środku, pod koniec bloku ✔️:
Optional<Node> optionalUnvisitedNodeWithLowestCost = getUnvisitedNodeWithLowestCost();
while (optionalUnvisitedNodeWithLowestCost.isPresent()) {
handleNode(optionalUnvisitedNodeWithLowestCost.get());
optionalUnvisitedNodeWithLowestCost = getUnvisitedNodeWithLowestCost();
}Polecam - mniej pisania 😊.
Metoda niżej dokonuje wyboru węzła 🎯. Tutaj po raz kolejny korzystam z wygód jakie mi dają strumienie i programowanie funkcyjne 😌. Aby nie pisać dużo, opisuję króciutko każdy krok tej operacji 🔍:
var unvisitedNodesFromGraph = graph.stream().filter(node -> !node.isVisited()).toList();Skonwertuj na strumień, wyklucz odwiedzone węzły i skonwertuj na listę.
var unvisitedNodesFromTable = nodesTable.entrySet().stream().filter(entry -> unvisitedNodesFromGraph.contains(entry.getKey()));Skonwertuj tabelę z danymi na zbiór par klucz-wartość ("entrySet"), potem na strumień i wyklucz te pary, które nie występują w liście nieodwiedzonych węzłów (posługujemy się nazwą poprzez "getKey").
var unvisitedNodeTableRowDataWithLowestCost = unvisitedNodesFromTable.min(Comparator.comparing(entry -> entry.getValue().getCost()));Pobierz wiersz z naszej tabeli o najmniejszym odnotowanym koszcie ("min" od razu "ustala" odpowiedni element na podstawie podanego kryterium, a do porównywania kosztów używam "Comparator.comparing").
var optionalUnvisitedNodeWithLowestCost = unvisitedNodeTableRowDataWithLowestCost.map(Map.Entry::getKey);Pobierz obiekt węzła (używając klucza) z wyznaczonego wcześniej wiersza z tabeli (w postaci pary klucz-wartość).
return optionalUnvisitedNodeWithLowestCost.flatMap(unvisitedNodeWithLowestCost -> unvisitedNodesFromGraph.stream().filter(node -> node.getName().equals(unvisitedNodeWithLowestCost.getName())).findFirst());Jeżeli występuje jakakolwiek referencja, to wykonaj następującą czynność (wnętrze metody "flatMap"): skonwertuj na strumień, wyklucz te węzły, których nazwy nie zgadzają się z nazwą węzła o najniższym odnotowanym koszcie i zwróć pierwsze wystąpienie (które w tym przypadku będzie "tym jedynym" 👍). Jeżeli nie ma takiego węzła, to zwróć "null" 🚧. W tym miejscu jest zwracana wartość w postaci wybranego węzła do zbadania jego sąsiadów (uff... 😅) ❤️.
Zobacz na typ zwracanej wartości przez tę metodę:
Optional<Node>"Optional" w języku Java stanowi "otoczkę" wokół referencji, która może być wartością "null". To ma na celu zabezpieczyć kod przed próbą robienia czegokolwiek na referencji, która może być równa "null" ✅.
Idźmy dalej 🥾.
Po upewnieniu się, że znaleziono węzeł o najniższym odnotowanym koszcie, wchodzimy do kolejnej metody, na której wykonujemy już realne działania ▶️. Mianowicie:
- wypisujemy komunikat o aktualnie obsługiwanym węźle,
- wywołujemy metodę do obsługi wszystkich węzłów sąsiednich danego węzła,
- oznaczamy węzeł jako "odwiedzony".
Przyglądając się metodzie do obsługi sąsiadów, widzimy tę instrukcję:
nodeNeighbours.entrySet().forEach(neighbourDataFromGraph -> updateNodesTableRowDataIfNeeded(neighbourDataFromGraph, node));Na język polski: skonwertuj słownik węzłów sąsiednich na pary klucz-wartość i dla każdego z nich wywołaj metodę z dwoma parametrami.
I już do niej przechodzimy, która jest ostatnią częścią naszego algorytmu Dijkstry 😁!
Pobieramy sobie serię danych, które oznaczają kolejno:
- obiekt węzła grafu pobrany z pary klucz-wartość,
- koszt rzeczywisty węzła z grafu pobranego z pary klucz-wartość,
- wiersz danych z tabeli dotyczący węzła "rodzica",
- wiersz danych z tabeli dotyczący węzła sąsiedniego,
- odnotowany koszt węzła "rodzica" pobrany z wiersza danych,
- odnotowany koszt węzła sąsiedniego pobrany z wiersza danych,
- suma odnotowanego kosztu węzła "rodzica" z wiersza danych i kosztu rzeczywistego węzła sąsiedniego z grafu.
Abyś mógł/mogła dostrzec różnice w pobieranych wartościach, zamalowałem odpowiednie frazy różnymi kolorami 🎨.
Pomijając wywołania metod do wypisywania komunikatów, doszliśmy do kluczowej instrukcji warunkowej zadającej ważne pytanie: "czy dotychczasowy odnotowany koszt węzła sąsiedniego, jest większy od sumy odnotowanego kosztu węzła "rodzica" z wiersza danych i rzeczywistego kosztu przejścia do węzła sąsiedniego pobranego z grafu?".
Jeżeli tak, to to oznacza, że znaleźliśmy krótszą ścieżkę do tego grafu i należy zaktualizować nasze notatki ‼️. Wówczas aktualizujemy nasz wiersz w tabeli przypisując nowy (mniejszy) koszt, a za węzeł "rodzica" przypisując węzeł, który wyznaczyliśmy na samym początku w pętli "while" (ten o najmniejszym odnotowanym koszcie) 👍.
Algorytm Dijkstry powtarza w kółko te same opisane czynności (od wyznaczenia węzła o najniższym koszcie, do aktualizacji wpisów w tabelce), aż wyczerpią się wszystkie nieodwiedzone węzły i na tym kończy swoje działanie 🏁. To jest równoznaczne z zakończeniem programu ☑️.
Nie złość się drogi Czytelniku, jeśli masz ogromne problemy ze zrozumieniem co się tu wyprawia 😀. Jeżeli tak jest, to narysuj sobie na kartce wszystko krok po kroku i skorzystaj z kolorowych mazaków 🎨. Wszystko stanie się jasne 😉.
Dotarliśmy do mety (już bez algorytmu 😉). Nie pytaj ile czasu mi zajęło, żeby powstał ten artykuł 😅. Algorytm Dijkstry wymagał ode mnie rozpisania na wielkiej kartce A4, abym pojął jakim "cudem" to działa 🎉.