Uwaga, sięgamy dziś po drugi problem algorytmiczny do rozpatrzenia. Bardzo znany i bardzo ciekawy problem, który posiada pięknie brzmiącą nazwę "problem wędrującego komiwojażera". Musieliście usłyszeć o nim chociaż raz w życiu, jest aż tak popularny. Rozpatrzymy dzisiaj dwie wersje algorytmów: rozwiązujący ten problem w sposób dokładny i aproksymacyjny. Brzmi nieźle? To wchodźcie do środeczka!
| Tweet |
PROBLEM WĘDRUJĄCEGO KOMIWOJAŻERA NIE DA SIĘ TAK PROSTO ROZWIĄZAĆ...
OK, postraszyłem nagłówkiem jednak najpierw wprowadzę w temat. "Travelling salesman problem" opisuje przypadek tytułowego komiwojażera, który musi odwiedzić kilka miast / miejscowości / [tu wstaw własny odpowiednik]. Główną ideą jest odpowiedź na pytanie w jakiej kolejności odwiedzić wszystkie miasta, tak żeby dystans całej wędrówki był jak najkrótszy. Od strony algorytmicznej stanowi to twardy orzech do zgryzienia i tu nie chodzi o brak znanej na to metody. Metoda jest...tylko że wysoce nieefektywna!
Problem: opracowanie najkrótszej drogi do odwiedzenia wszystkich lokalizacji
NIE DA SIĘ INACZEJ
Wyobraźmy sobie, że mamy 5 miasteczek do zbadania. Uznajmy również, że nie wybieramy żadnej pozycji startowej, czyli jesteśmy zmuszeni do sprawdzenia każdej, ale to dosłownie KAŻDEJ kombinacji. To co, wystarczy policzyć wszystkie i git? No nie jest tak kolorowo ;)!
 |
Aby rozwiązać problem wędrującego komiwojażera w sposób dokładny, trzeba sprawdzić WSZYSTKIE możliwe kombinacje!!! Podejście takie nazywa się "brute-force".
Źródło: Wikipedia
Metoda na piechotę jaka została tu przedstawiona nosi nazwę "brute-force" i chodzi w niej o przeczesanie każdej dozwolonej kombinacji i zwróceniu takiego rozwiązania, który przynosi najlepsze rezultaty. Dokładność rozwiązania, gwarantowana. Prędkość wykonywania, fatalna! Dysponując tylko pięcioma lokacjami do zbadania bez wybierania pozycji startowej, program musi zmierzyć aż 120 kombinacji i spośród nich wybrać trasę najkrótszą!!! Skąd wiemy, że właśnie tyle?
Selekcja poszczególnych miast jeden po drugim do złudzenia przypomina permutację bez powtórzeń (dział kombinatoryki się kłania). Jest to ciąg utworzony ze wszystkich elementów danego zbioru (jakim są lokacje do zbadania). Stąd też, mając do wyboru 5 miast:
C = {a, b, c, d, e}
to jedną ze 120 kombinacji będzie taki ciąg:
abcde
ale to również będzie to:
acbde
i to:
abced
i tak dalej. Nie wysilajcie się z policzeniem wszystkich dostępnych kombinacji:
Pn = n!
Wynika stąd, że:
P5 = 5! = 120
Trochę dużo, prawda? Trochę BARDZO dużo, jak na zbiór 5-elementowy. A im dalej w las, tym jeszcze gorzej! Stąd też złożoność obliczeniowa tego problemu wynosi nic innego jak O(n!) i charakteryzuje się wykładniczym wzrostem w czasie!!! Z tego powodu, problem wędrującego komiwojażera to "problem NP-zupełny", o którym napiszę dużo więcej w osobnym artykule. Wniosek jest jednoznaczny - "brute-force" kompletnie się nie nadaje dla dużego zbioru danych.
Nawet jeśli przyjąć, że zaczynamy od jakiegoś określonego miejsca, to obetniemy obliczenia tylko o jedno "oczko" w silni, więc:
4! = 24
Jak na piątkę miast, to jeszcze OK tylko dla większej liczby już się nie wywiniecie i liczba kombinacji będzie już nie do przyjęcia (6! = 720)!
Problem: opracowanie najkrótszej drogi do odwiedzenia wszystkich lokalizacji przy jednoczesnym uniknięciu badania wszystkich dostępnych kombinacji
CZY JESTEŚMY SKAZANI NA PORAŻKĘ?
Skąd. Po prostu trzeba przejść na inną metodę o nieco mniejszej dokładności, ale za to o wiele większej skuteczności w działaniu. I tu dotykamy podejścia aproksymacyjnego, czyli metodyki zdolnej do znalezienia rozwiązania zbliżonego do dokładnego. Ono może być zadowalające, ale nie mamy pewności że takie będzie zawsze (może być nawet "wyjęte z czapki"). Kolejne słówko jakie radzę zapamiętać: "heurystyka".
Problem wędrującego komiwojażera można spróbować rozwiązać dużo oszczędniej. Weźmy pod lupę jeszcze raz te 5 miast. W ramach podjęcia próby otrzymania rozwiązania przybliżonego, możemy na ten przykład wybrać na początek losowo jeden z punktów:
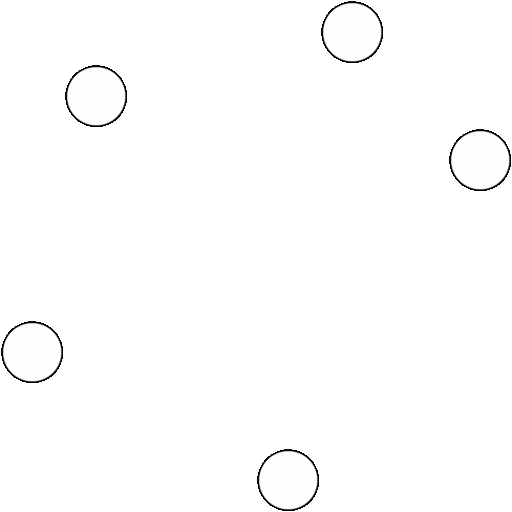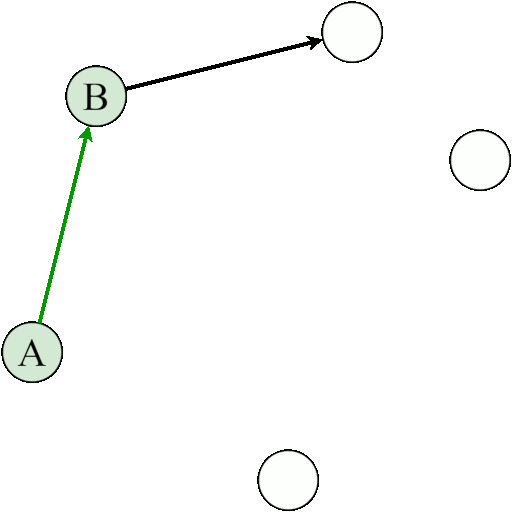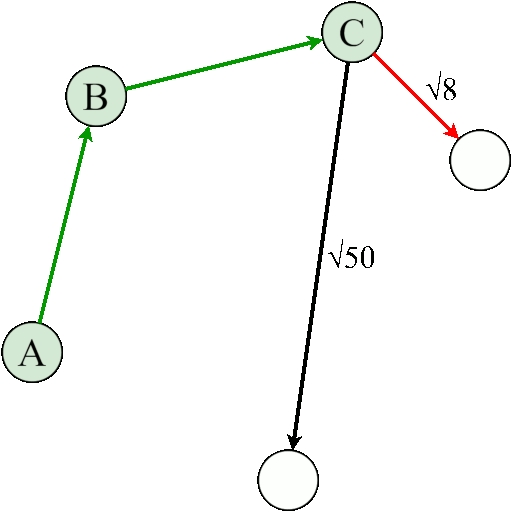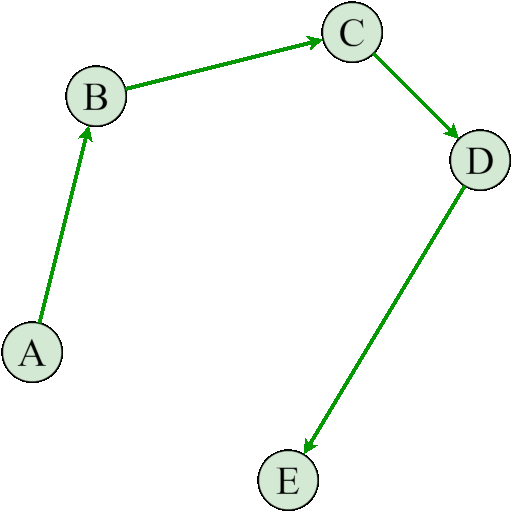 |
Podejście algorytmu aproksymacyjnego rozwiązującego problem wędrującego komiwojażera.
i sprawdzać resztę z nich po kolei która odległość od tego wybranego do czterech pozostałych będzie jak najmniejsza. Później konsekwentnie wykreślać pozycje z listy, aż będzie pusta i w taki oto sposób otrzymujemy wynik ostateczny. Powtórzę się - nie ma pewności przy tym podejściu, że wynik będzie rewelacyjny. Aproksymacja tym się charakteryzuje, że rozwiązanie jest obarczone pewnym błędem. On może być mniejszy lub większy, aczkolwiek w większości przypadków on występuje. Natomiast w ramach rekompensaty, zyskujemy na znacznym zredukowaniu złożoności obliczeniowej, bowiem to podejście będzie nas kosztowało "jedynie" O(n2) podejść w najgorszym przypadku. Kwadrat jest dlatego, gdyż dla każdego miasta w którym się aktualnie znajdujemy (to jest to pierwsze wylosowane), musimy porównać odległość z każdym innym miastem, które dalej jest niewiadomą. Lista każdorazowo się skraca (więc to nie będzie de facto n*n za każdym razem), jednak w notacji dużego O stałe nie grają roli, zatem mamy n do kwadratu.
KOD ŹRÓDŁOWY
Złóżmy to sobie do kupy podsumowując kodem źródłowym prezentującym podejście aproksymacyjne. Sprawdźcie sobie i poeksperymentujcie z różnymi kombinacjami:
KLASA "MAIN"
public class Main {
public static void main(String[] args) {
new TravellingSalesmanProblem();
}
}REKORD "POINT"
public record Point(int x, int y) {
public int distanceTo(Point point) {
int x = this.x - point.x;
int y = this.y - point.y;
int squaredX = x*x;
int squaredY = y*y;
double distance = Math.sqrt(squaredX + squaredY);
return (int)Math.round(distance);
}
}REKORD "CITY"
public record City(String name, Point position) {
@Override
public int hashCode() {
return name.hashCode();
}
@Override
public boolean equals(Object o) {
if(getClass() != o.getClass()) {
return false;
}
City city = (City)o;
return name.equals(city.name);
}
public int distanceFrom(City city) {
return position.distanceTo(city.position);
}
}KLASA "TRACK"
import java. util.LinkedHashSet;
public class Track extends LinkedHashSet<City> {
public int totalDistance(City startCity) {
int distance = 0;
for (City city : this) {
if(!city.equals(startCity)) {
distance += city.distanceFrom(startCity);
}
}
return distance;
}
}KLASA "CITIES"
public class Cities extends HashSet<City> {
public Cities() {
add(new City("Warszawa", new Point(-40, 320)));
add(new City("Kielce", new Point(3280, 6709)));
add(new City("Kraków", new Point(456, 746)));
add(new City("Szczecin", new Point(7000, -658)));
add(new City("Wrocław", new Point(15000, -8900)));
}
public City closestCity(City startCity) {
City closestCity = null;
int shortestDistance = Integer.MAX_VALUE;
for (City city : this) {
int distanceFromStartCity = city.distanceFrom(startCity);
if(distanceFromStartCity < shortestDistance) {
closestCity = city;
shortestDistance = distanceFromStartCity;
}
}
return closestCity;
}
public City randomCity() {
City[] array = toArray(new City[0]);
int index = randomCityIndex();
return array[index];
}
private int randomCityIndex() {
Random random = new Random();
return random.nextInt(0, size());
}
}KLASA "TRAVELLINGSALESMANPROBLEM"
import java. io.PrintStream;
public class TravellingSalesmanProblem {
private final Track track = new Track();
private final Cities cities = new Cities();
private final City startCity = cities.randomCity();
private final PrintStream printStream = System.out;
private City currentCity;
public TravellingSalesmanProblem() {
addCityToTrack(startCity);
printStream.println("Wybrane miasto startowe: " + startCity.name());
selectCities();
printStream.println("TRASA: ");
track.forEach(c -> printStream.println(c.name()));
printStream.println("Dystans: " + track.totalDistance(startCity));
}
private void selectCities() {
while (!cities.isEmpty()) {
addClosestCity(currentCity);
}
}
private void addClosestCity(City startCity) {
City closestCity = cities.closestCity(startCity);
if(closestCity != null) {
printStream.println("Najbliższe miasto to " + closestCity.name() + ". Odległość wynosi " + closestCity.distanceFrom(startCity) + ".");
addCityToTrack(closestCity);
}
}
private void addCityToTrack(City city) {
track.add(city);
cities.remove(city);
currentCity = city;
}
}Z uwagi na rozległość kodu, tłumaczę zgodnie z kolejnością od góry do dołu. Pomijając oczywistość klasy "Main", mamy rekord dla punktu w układzie kartezjańskim. BTW, rekord w języku Java jest zwięzłym skrótowcem dla klas dysponujących danymi składowymi niemodyfikowalnymi (ze słowem kluczowym "final") wraz z ich akcesorami, czyli metody typu "get". W jego wnętrzu znajduje się jedyna metoda kalkulująca dystans pomiędzy dwoma punktami. To ma pełnić funkcję pomocniczą, aby znów oddzielić ziarno od plew.
Dalej mamy drugi rekord przeznaczony dla obiektów miasta, czyli tych naszych lokacji jakie komiwojażer musi odwiedzić. Przesłoniłem metody "hashCode" i "equals", ponieważ do eksperymentu wykorzystałem zbiór ("LinkedHashSet"), kolekcję zdolną do przechowywania wyłącznie obiektów unikatowych. "LinkedHashSet", poza wymienioną cechą, zapamiętuje również kolejność wprowadzanych rekordów. Oprócz tego, dodałem metodę obliczającą odległość między miastami, aby nie bawić się w łańcuszki "getter'ów" do obiektów typu "punkt".
Schodząc niżej, trafiamy na klasę potomną dziedziczącą również od "LinkedHashSet", która odpowiada za planowanie trasy komiwojażera. Nie ma tu niczego zaskakującego, jedyna metoda która kalkuluje całkowitą odległość trasy przechodząc od miasta do miasta. "LinkedHashSet" MUSI BYĆ, gdyż kolejność dodawanych elementów musi być zachowana, co w przypadku budowania trasy jest kluczowe!
"Cities" jest kolejną klasą dziedziczącą tym razem od zwykłego "HashSet" (w przeciwieństwie do poprzednika, nie przechowuje kolejności w jakiej dodaje się elementy). Wewnątrz konstruktora wprowadziłem parę przykładowych miast jakie występują w naszym kraju. Współrzędne wpisałem już odbiegające od rzeczywistości, aby nie bawić się w geografa i nie przeciągać drobnego punktu na parę dni. Zawartość jest już ciut bardziej rozbudowana. Zaraz po konstruktorze, mamy metodę która zwraca najbliższe miasto spośród dostępnych od danego miasta. Dodałem również metodę zwracającą losowo jedno z miast na potrzeby pierwszego kroku (jakim jest losowe wybranie jednej z opcji) i dodatkowo wydzieliłem metodę losującą miasto od metody losującej indeks elementu.
Aż docieramy do klasy uruchomieniowej, w której mamy istotę sprawy czyli problem wędrującego komiwojażera. Dane składowe składają się z instancji obiektu trasy, obiektu miast do zbadania oraz uwaga, losowo wybierane miasto oraz miasto rozpatrywane w danej iteracji (to akurat jest potrzebne do śledzenia aktualnego miejsca, które będzie się zmieniać co wybór lokacji). Patrząc na konstruktor, mamy tam natychmiastowe dodanie wybranego losowo miasta do trasy, jako że to będzie nasz pierwszy punkt. Pomijając instrukcje wypisujące informacje na terminal, mamy metodę "selectCities" w której dzieje się rzecz najważniejsza - dobieranie kolejnych lokalizacji na podstawie odległości w przestrzeni kartezjańskiej.
Wewnątrz pętli "while" sprawdzającej na bieżąco czy zostały jeszcze jakiekolwiek miasta do zbadania, mamy wywołanie kolejnej metody której zadaniem jest znalezienie i zwrócenie najbliższego miasta od aktualnej lokacji (składowa "currentCity"). Jeżeli algorytm znalazł takową, to dodaje to samo miasto do trasy (usuwając jednocześnie z listy dostępnych miast) i przypisuje referencję do "obecnego miasta". Wszystko wykonuje się raz po raz, aż do wyczerpania listy niezbadanych miast.
To, co zaprezentowałem, stanowi jedno z co najmniej kilkunastu podejść aproksymacyjnych, czyli alternatywnych algorytmów zwracających rozwiązanie przybliżone. Przypominam, że korzystamy z aproksymacji dlatego, żeby uniknąć nieakceptowalnej złożoności czasowej mogącej przynieść rozwiązanie nawet po kilkuset latach (kieruję do notacji dużego O)!
Na tym zakończę omawiać problem wędrującego komiwojażera. Zagadnienie same w sobie ciekawe wymagające podejścia bardziej inteligentnego niż "brute-force" i latanie po wszystkich kombinacjach jak leci.