Temat dzisiejszego artykułu z algorytmiki: notacja dużego O i jej interpretacja opisana w sposób łopatologiczny. Jeśli głowicie się już nad samym hasłem, to wchodźcie a nie pożałujecie!
| Tweet |
NOTACJA DUŻEGO O ZMIERZY CI CZAS DZIAŁANIA ALGORYTMU
Termin może dziwaczny, a już z pewnością enigmatyczny na pierwszy rzut oka. To jest miara szybkości danego algorytmu. Zgodnie z moją wypowiedzią w artykule wprowadzającym dziedzinę algorytmiki, napisałem że to jest również sztuka badania ich efektywności. Jednym z kryteriów jest czas na znalezienie rozwiązania (innym czynnikiem jest między innymi dokładność i komórki pamięci, ale o tym innym razem). Notacja dużego O pozwala zmierzyć czas działania określonego algorytmu na podstawie liczby operacji do wykonania wraz z rosnącym rozmiarem danych wejściowych! Nie, jak mogłeś/mogłaś pomyśleć, w milisekundach czy w innej metryce czasowej. Miara określana jest jako tempo wzrostu liczby instrukcji.
Należy wspomnieć, że notacja dużego O opisuje złożoność czasową w przypadku najgorszym. Najgorszym, czyli sytuacja w której liczba wykonanych operacji osiągnęła maksimum przedstawiane właśnie przez tę notację. Nie wszystkie algorytmy wyczerpują liczbę instrukcji do granic wytrzymania. Poznany niedawno algorytm wyszukiwania binarnego charakteryzuje się złożonością czasową O(log(n)), więc dla stuelementowej tablicy w najgorszym przypadku wykona się 7 iteracji celem znalezienia rozwiązania. Jednak to wcale nie znaczy, że ZAWSZE będzie siedem. Rozwiązanie może zostać opracowane już za pierwszym razem (przypadek znalezienia szukanego elementu już od razu) i wtedy będzie przeczyć tej metryce (1 < 7). Mówimy wtedy o przypadku optymistycznym.
Notacja dużego O jest tylko jedną z kilku istniejących metryk opisujących złożoność obliczeniową, która stoi obok notacji "omega" czy notacji "theta", więc jeśli ktoś naprawdę posiada matematyczny łeb i chce pójść na całość z odkrywaniem tajemnic, to proponuję zainteresować się terminem jakim jest "asymptotyczne tempo wzrostu". Ja ponieważ należę do tych niekumatych z królowej nauk, wolę nie przekraczać tej granicy i skupić się na wyjaśnianiu tego tematu z informatycznej strony ;).
RODZAJE METRYK
Notacja dużego O może prezentować różnorakie metryki, jednak kilka z nich można wyróżnić jako często spotykane. Poznajmy parę zapisów:
- O(1)
- O(log(n))
- czas logarytmiczny (czyta się "logarytm z n przy podstawie 2")
- algorytm w najgorszym przypadku wykonuje tylko log2(n) instrukcji celem znalezienia rozwiązania
- przykładem jest algorytm wyszukiwania binarnego
- O(n*log(n))
- czas pseudowielomianowy
- algorytm w najgorszym przypadku wykonuje n*log2(n) instrukcji celem znalezienia rozwiązania
- przykładem jest sortowanie przez scalanie
- O(n2)
- czas kwadratowy
- algorytm w najgorszym przypadku wykonuje n2 instrukcji celem znalezienia rozwiązania
- przykładem jest sortowanie przez wybieranie
- O(n!)
- czas wykładniczy
- algorytm w najgorszym przypadku wykonuje n! ("n silnia") instrukcji celem znalezienia rozwiązania
- przykładem jest algorytm dokładny rozwiązujący problem wędrującego komiwojażera
Oto kilka przykładów często występujących notacji dużego O. Uprzedzam, że może przyjmować własne bardzo rzadko spotykane formy, jak na przykład:
O(⌊√n⌋*log(n))
Podłoga z pierwiastka z n przemnożona przez logarytm z n. Miałem taki algorytm na zajęciach.
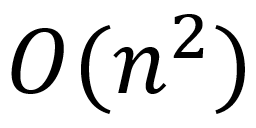 |
Notacja dużego O jest matematyczną miarą tempa wzrostu złożoności obliczeniowej (czasowej) wraz z rosnącym rozmiarem danych wejściowych. Im mniejszy wzrost, tym algorytm lepiej sobie poradzi przy ogromnych ilościach danych.
Dotarliśmy do mety. Notacja dużego O może być naprawdę ciekawym tematem do rozwinięcia i dobrym punktem zaczepienia w wyborze odpowiedniego algorytmu do naszych potrzeb projektowych. Trzeba jednak dobrze wgłębić się w temat z matematycznego punktu widzenia, aby zrozumieć skąd naprawdę się wzięły te metryki.